ベクトル磁気特性とは
高効率モータ実現のためにベクトル磁気特性解析技術を解説していきたいと思います。この技術は榎園正人教授(大分大学名誉教授、現在ベクトル磁気特性技術研究所代表)のご支援を受けており、教授が代表を務めるベクトル磁気特性技術研究所の情報を引用させて頂いています。
目次
1.ターゲットは電磁鋼板の鉄損低減
モータの出力は、体格(外径と厚み)、磁気量(磁束密度の大きさ)、電気量(コイルの巻き数と電流値)、回転数(回転スピード)の積に比例します(Fig.1-1)。モータ体格を小さく小型化し、同じ出力を得ようとすれば、残りの量を大きくする必要があります。ところが磁気量を大きくすれば鉄損が上昇。電気量を大きくすれば銅損が上昇。回転数を大きくすればやはり鉄損が上昇します。結果的に効率は下がってしまいます。
そこで、「何とか鉄損を減らす本質的な対策を打てないものか」というのが我々の課題で、ターゲットは電磁鋼板の鉄損低減です。これは変圧器にも当てはまります。


Fig.1-1 モータの出力式
2.鉄損は渦電流損とヒステリシス損の合計
鉄損は、渦電流損とヒステリシス損の合計になります。
渦電流損は電磁鋼板を薄くすることで減らすことが出来ます。例えば35H440という鋼材は、板厚さが0.35mmです。さらに薄く出来る技術が進歩すれば、渦電流損はかなり低減できると期待できます(Fig.2-1)。さらに、渦電流が減少する事により電磁鋼板内の反磁界成分が減少し、結果的に小さな磁界で磁束密度を高めるという効果が報告されています(Fig2-2)。この事は磁界励磁の為のコイル電流を小さく出来ることを意味し、銅損の低減が期待できます。
ヒステリシス損はヒステリシスカーブの面積に対応します。ところがヒステリシス損は若干の増加が起こります。そこで残るヒステリシス損の低減対策の課題が重要になってきます(Fig.2-3)。
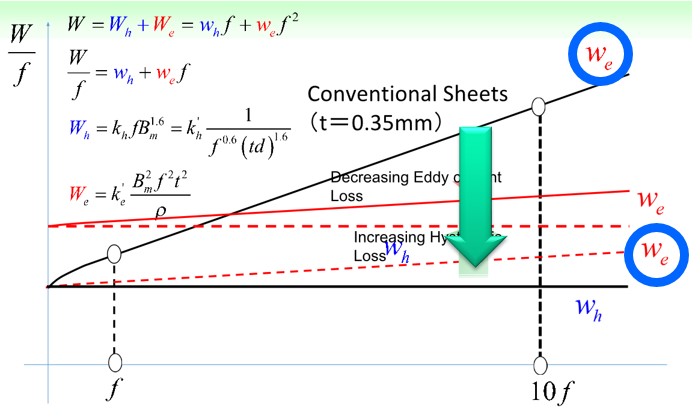
Fig.2-1 電磁鋼板の薄板化により渦電流損が減少
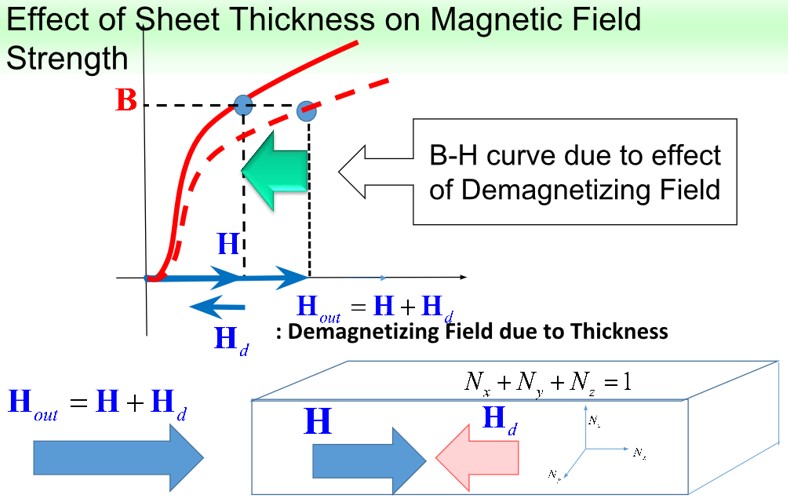
Fig.2-2 電磁鋼板の薄板化により磁気抵抗が減少
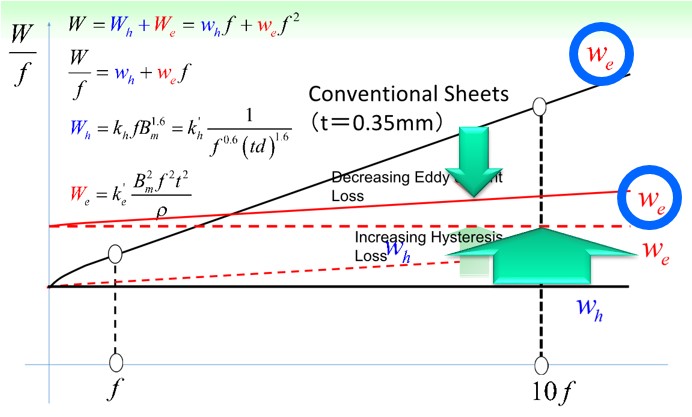
Fig.2-3 電磁鋼板の薄板化によりヒステリシス損が上昇
3.電磁鋼板のベクトル磁気特性
電磁鋼板の鉄損低減対策ですが、従来は以下の方法でした。電磁場解析で磁束密度の分布を算出。鉄損式(磁束密度のべき乗に比例)を使って鉄損分布と鉄損量を推定する(Fig.3-1)。では鉄損を下げる設計は、磁束密度を下げるしかないのです。このように従来のやり方では行き詰ってきました。
実際にはモータコアに使われる電磁鋼板内部では、絶えず磁束密度と磁界が変化しています。場所によって交番磁束(磁束密度が一方向に変化する)や回転磁束(磁束密度が回転)が発生しています。同様に磁界も変化していますが、詳細に測定すると、磁束密度と磁界の向きがズレています。例えば回転磁束に先行して磁界が回転したり、途中で遅れたり。このように磁束密度と磁界の関係は、大きさだけでなく向き(ベクトル)も考慮しないと正確に表現できないのです(Fig.3-2)。
精密に測定できる技術が出来てみたら、磁界Hと磁束密度Bはベクトル関係であった。その結果ヒステリシスループが描け、その面積が鉄損なのだから、このベクトル磁気特性を把握する事が非常に重要だという事がわかってきました。
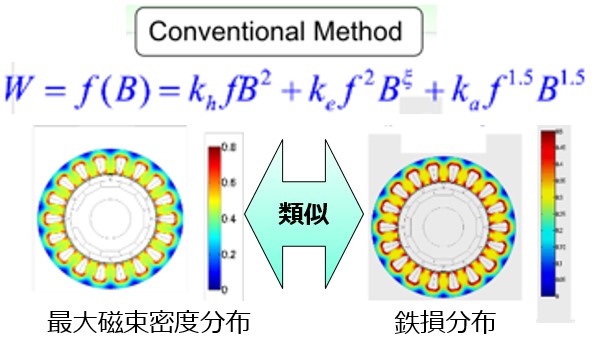
Fig.3-1 鉄損式では磁束密度と鉄損が類似分布
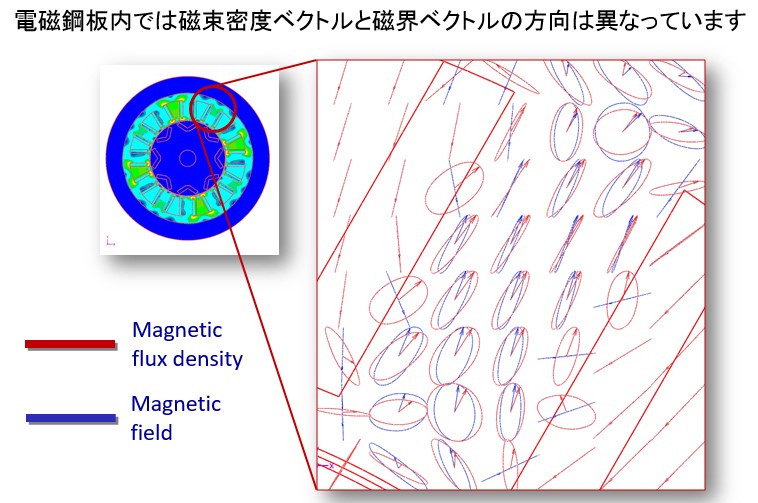
Fig.3-2 磁界Hと磁束密度Bベクトルによるリサージュ波形
4.従来の測定はスカラ磁気測定
現状の材料測定方法はスカラ磁気測定と言われます。エプスタイン試験器や単板磁気試験器は、一方向に励磁してその方向の磁束密度と磁界の大きさの関係を測定するものです。それにより得られるのがBHカーブです。この情報を基に磁場解析を行うのですから、スカラ磁場解析という事になります。電磁鋼板を様々な方向に切り出し、その試料の方向毎の磁気特性を測定しても、スカラ磁気測定でスカラ磁場解析(ただし異方性として考慮)なのです。
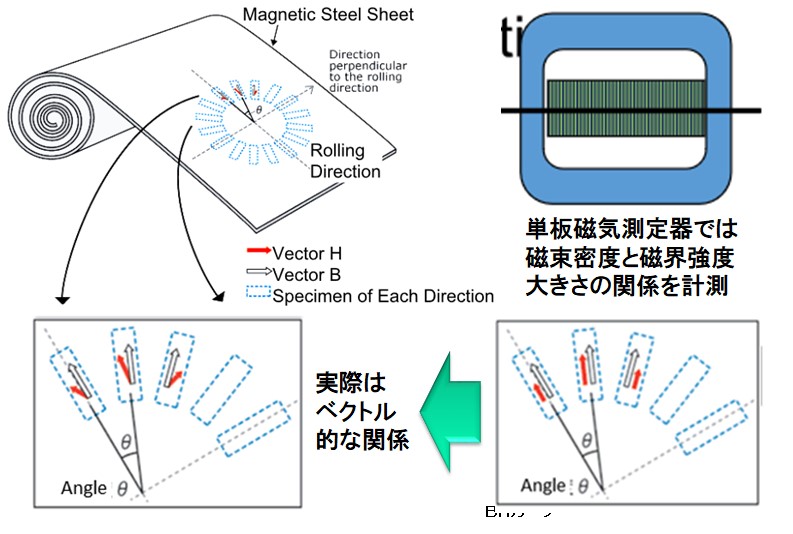
Fig.4-1 現状の測定はスカラ磁気測定
5.開発されたベクトル磁気測定装置
モータや変圧器の電磁鋼板内には交番磁束や回転磁束が発生しています。交流で励磁しているので、電気角一周期で一回転しています。交番磁束はある方向に対してのみ、正弦波的に磁束密度ベクトルが伸び、続いて縮み、今度は反対向きに伸びて縮むという変化をしています。ところがこの時も磁界ベクトルの軌跡は2次元面で膨らむことが観測できます(Fig.5-1)。これは磁界ベクトルが磁束密度ベクトルと違う方向に向いている事を表しています。スカラ磁気測定では観測できないベクトル磁気特性です。
そこで交番磁束や回転磁束を発生させて、その時々の磁界を測定する2次元ベクトル磁気測定装置が開発されました(Fig5-2)。電磁鋼板の試料に対して圧延方向とそれに直角方向に励磁ヨークを配置し、交番磁束や回転磁束を発生させ磁界強度を測定するものです。これにより電磁鋼板の磁気特性情報はスカラからベクトルへと飛躍します。現在、メトロン技研様がベクトルBHテスターとして商品化しています(Fig.5-3)。電磁鋼板の圧延方向も考慮した正確な材料特性が得られます。この材料特性を使って鉄損解析をするのが、ベクトル磁気特性解析です。例えば、従来得られなかった正確なヒステリシス損分布を計算できるようになります。
Fig.5-1 交番磁束に対する回転磁界(50A470,1.3Tesla)
Fig.5-2 2次元ベクトル磁気測定装置
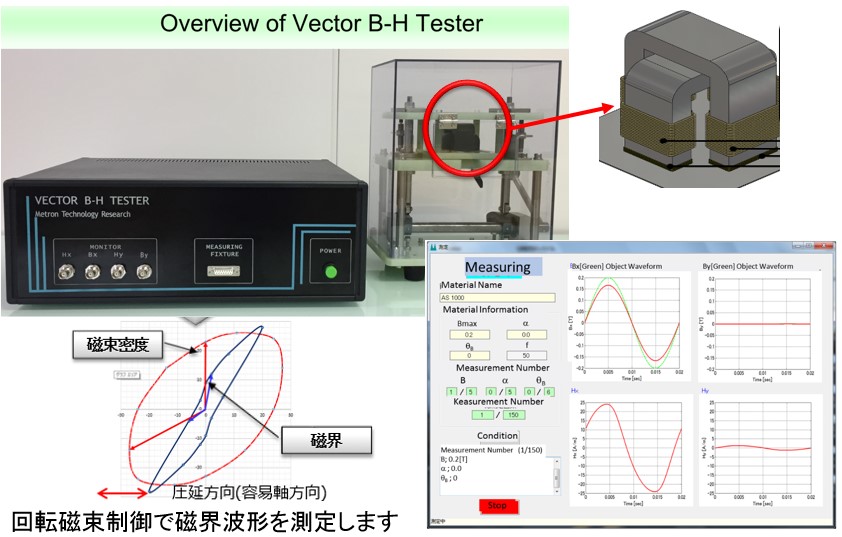
Fig.5-3 ベクトルBHテスター(メトロン技研様提供)
6.実際の測定結果
2次元ベクトル磁気測定装置で実際に測定した結果です(Fig6-1)。 回転磁束密度ベクトル(赤印)を1.0Tの大きさで真円に回転するように制御しています。その時の磁界強度ベクトル(青印)の回転軌跡です。電磁鋼板の圧延方向はX軸方向に設定してあります。
無方向性電磁鋼板でも、圧延方向と直角方向で異方性が見られます。圧延方向は磁化容易方向の傾向が有り、磁束密度1.0Tを得るための磁界強度は小さくて済みます。直角方向に対しては大きな磁界強度で磁束密度1.0Tを達成できますので、磁界のリサージュ波形は縦長になります。この傾向は方向性電磁鋼板、2方向性電磁鋼板でさらに顕著になります。そしてベクトル向きも異なっています。このような計測が出来るようになったわけです。
そしてこれらを磁気特性データとして活用しようとして、まずはデータベース化します。そしてそのデータベースを、スカラ磁場解析のBHカーブのように活用するのが、ベクトル磁気特性解析技術です。
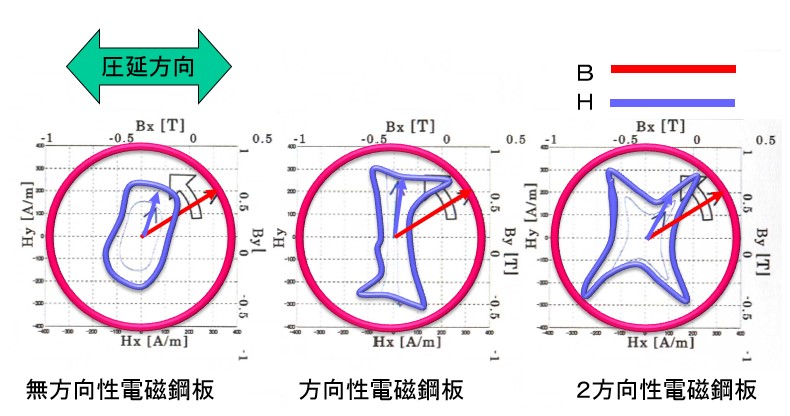
Fig.6-1 電磁鋼板の種類によるベクトル磁気特性の違い
7.磁気特性としてデータベース化
ベクトル磁気測定装置を使って、電磁鋼板の試料に対して、交番磁束や回転磁束を発生させて、それに対応した歪磁界強度波形を多数測定し、ベクトル磁気特性データベースとして登録します。データは3つのパラメータにより整理します(Fig.7-1)。
回転磁束は真円から楕円さらには面積を持たない交番磁束まで表現するために、楕円の長軸の磁束密度Bmaxと短軸のBminの比を軸比αとします。α=1が真円でα=0が交番磁束になります。次に回転磁束の楕円の向きですが、圧延方向に対して何度反時計方向に傾いているかを傾角θBとします。最後に、最大磁束密度Bmaxの大きさ自体を例えば0.0Teslaから1.6Teslaに変化するパラメータにします。例えば、軸比10点、傾角19点、最大磁束密度17点の3230種類の条件で、電気角一周期分の歪磁界強度波形を保存します。実際には歪磁界強度波形はフーリエ級数で表現してあり、最大次数は51次とかの例があります。このデータベースの容量は100Mb前後になります。
この磁気特性データは非常に貴重で、ここから様々の情報を見る事が出来ます(Fig.7-2)。例えば傾角に対する鉄損特性とか、スカラBHカーブもこの中の情報に含まれているわけです。ホームページでは「磁気特性の見える化」として、その特性チャートを展開していこうと考えています。そして、このデータベースを参照してベクトル磁気特性解析が行われます。
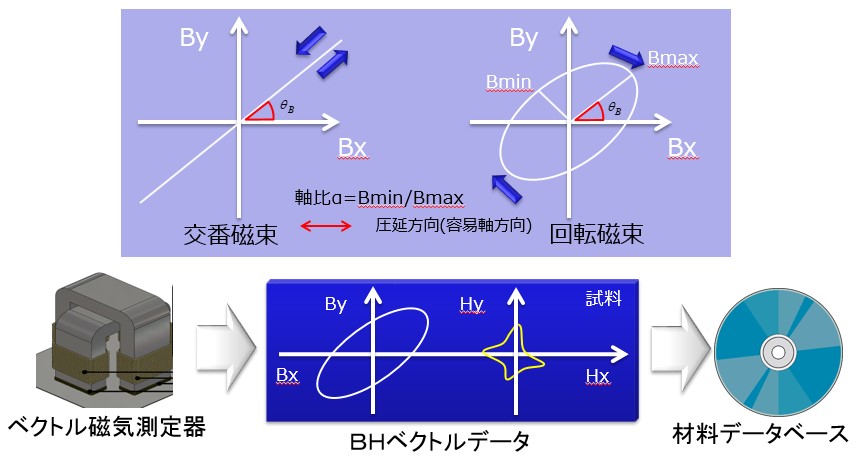
Fig.7-1 2次元ベクトル磁気特性データベース
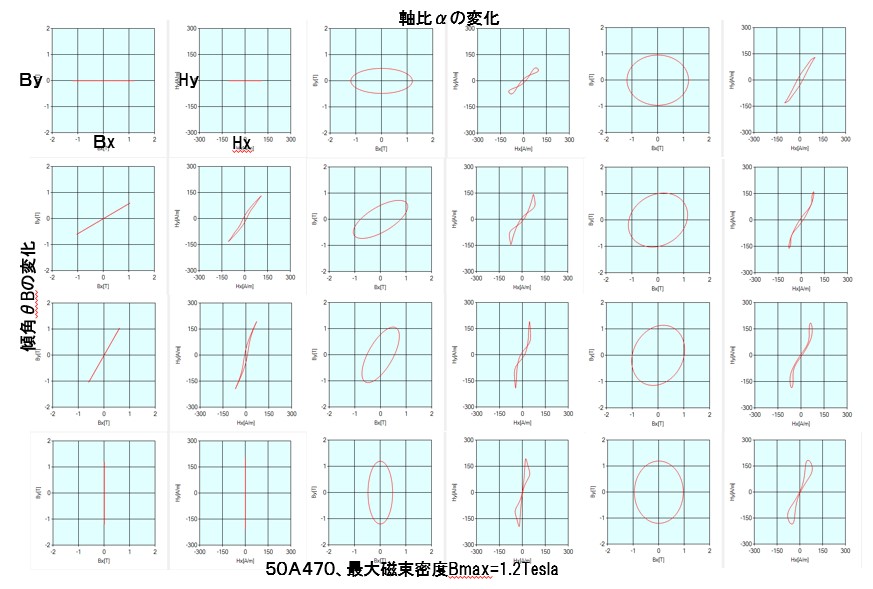
Fig.7-2 パラメータ変化時の磁束密度と磁界強度のリサージュ波形
8.E&Sモデルとは
E&Sモデルとは、先の2次元ベクトル磁気特性で得られた磁束密度ベクトルBと磁界強度ベクトルHの関係を表現する数値モデルです。さらに有限要素法を用いた磁気特性解析に適用したアルゴリズムと考えていただいて良いと思います。
E&SモデルのBとHの関係式を示します(Fig.8-1)。このモデルは磁束密度波形に磁気抵抗係数(νxr、νyr)を乗じたものと、磁束密度波形の積分波形に磁気ヒステリシス係数(νxi、νyi)を乗じたものの和を計算する事で磁界強度波形を求める手法になります。磁気ヒステリシス係数がある事によって、BxとByが同時にゼロになるような条件の時も、磁界強度は値を持つことが出来るように設計されています。磁気抵抗係数と磁気ヒステリシス係数は、ベクトル磁気特性データベースに格納されている各条件(Bmax、θB、α)の磁束密度・磁界強度波形から計算されます。τは電気角一周期の分割点で、磁気抵抗係数等も電気角一周期分の波形になります(Fig.8-2)。実際の計算では、磁束密度波形も磁界強度波形もフーリエ級数に展開し演算する事により、磁気抵抗係数と磁気ヒステリシス係数のフーリエ係数が決定でき、最後に時間軸波形に戻しています。この計算の演算時間は掛かりません。
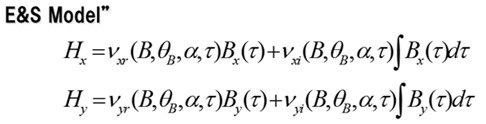
Fig.8-1 E&SモデルのBとHの関係式
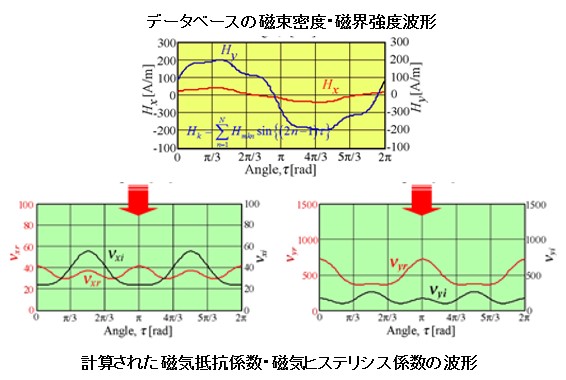
Fig.8-2 磁気抵抗係数と磁気ヒステリシス係数の波形
9.E&Sモデルのフローチャート
E&Sモデルの計算は、回転磁束(電気角)一周期分が基本になります。フローチャートを示します(Fig.9-1)。まず初期条件で一周期分の磁場解析を行います。各要素ごとの磁束密度の波形結果からフーリエ級数的に基本波形を取り出します。この基本波形から最大磁束密度Bmax(長軸の値)、最少磁束密度Bmin(短軸の値)、傾角θB(圧延方向とBmaxの角度)、軸比α(Bmax/Bmin)を求めます。この情報を基にデータベースから対応する回転磁束を見つけ出し、その時の磁界波形を抽出します。磁束密度と磁界から一周期分の磁気抵抗係数、磁気ヒステリシス係数波形を算出し、これを使って2回目の一周期分の磁場解析を行います。これを収束(波形の変化が充分小さくなる)するまで行います。収束した結果は、各要素毎に実測で求めた材料特性に沿った結果になります。最後に磁束密度・磁界波形からヒステリシスカーブを求め、鉄損を算出します。ベクトル磁気特性解析全体の流れを示します(Fig.9-2)。
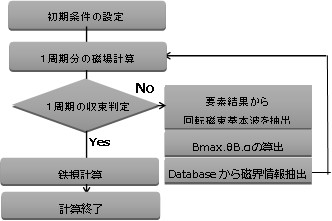
Fig.9-1 E&Sモデルのフローチャート
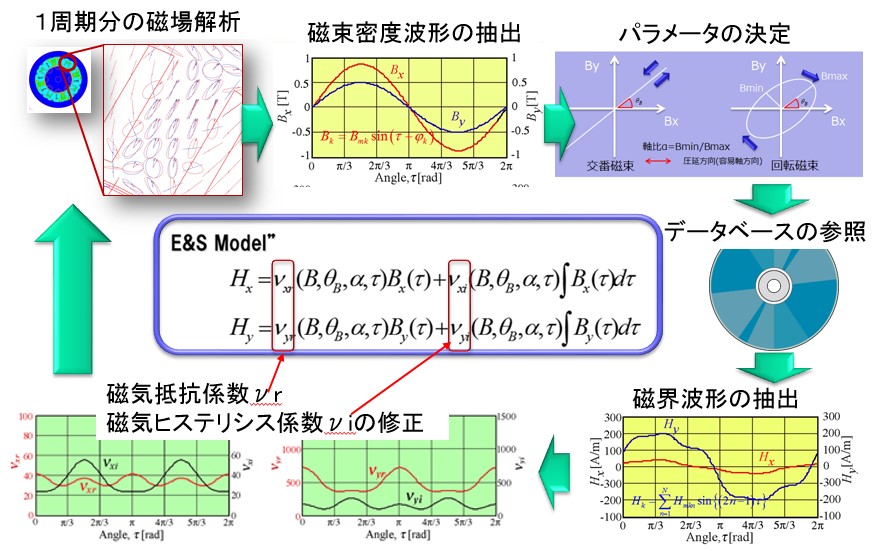
Fig.9-2 ベクトル磁気特性解析全体の流れ
10.圧延方向を考慮した解析
電磁鋼板は、無方向性(例では50A470)でも圧延方向に磁束が通りやすく、それに直角方向は通りにくい傾向があります。それをベクトル磁気特性解析で再現します(Fig.10-1)。
リング状に切り抜いた電磁鋼板にコイルを巻いて励磁するモデルです。圧延方向はX軸(横方向)です。ベクトル磁気特性解析の結果コンター図を示します。磁束密度分布は周方向にほぼ均一です、磁路長の短い内径側が大きな値になっています。これに対して磁界分布は左右部分に大きな値が出ています。これは磁束密度ベクトルがX軸を向いて圧延方向にそろっている上下部分では磁束が通りやすく、小さな磁界でも結果の磁束密度になるためです。逆に左右部分では磁束の流れと圧延方向が直角で磁束が通りにくく、大きな磁界で結果の磁束密度を達成するからです。磁束密度と磁界から得られる鉄損分布も、圧延方向の影響を受けて左右部分に大きな値が出ています。
従来のスカラ磁気特性解析では得られない結果が、ベクトル磁気特性で計算できる基本問題です。
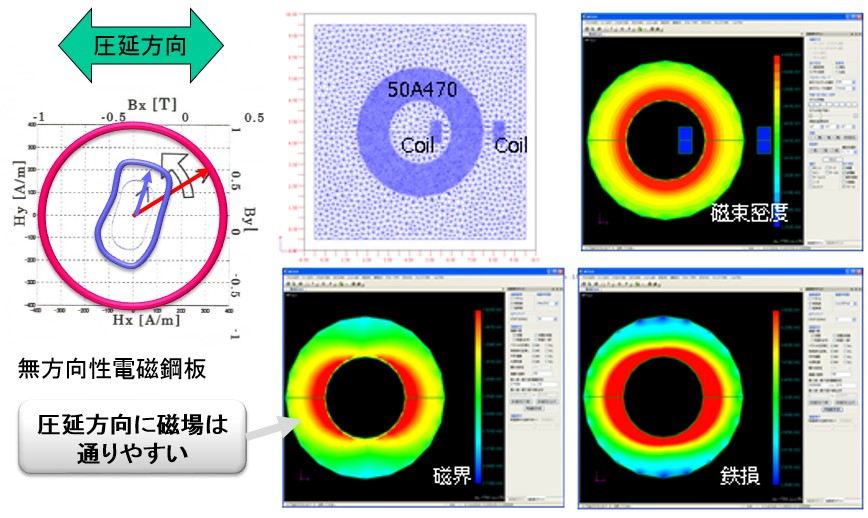
Fig.10-1 圧延方向の影響
11.従来解析法との比較
従来のスカラ磁気特性解析の鉄損算出法では、磁束密度の結果から鉄損式を使った後処理で鉄損分布を求めていました。従って、磁束密度分布と鉄損分布は類似分布になります。これに対してベクトル磁気特性解析では鉄損分布は磁束密度分布と異なってきます。これは圧延方向の磁気特性の影響を考慮した解析だからです(Fig.11-1)。またヒステリシスを考慮した鉄損解析でも、ヒステリシス材料特性がスカラ測定から得られたものでは正確な鉄損分布は得られません。ベクトル磁気特性解析では、磁界分布が正確に計算できる特徴があります。ベクトル磁気特性データベースの磁束密度と磁界強度の測定されたデータを参照しているからです(Fig.11-2)。さらに、その磁束密度波形と磁界強度波形からヒステリシスループが描け、その面積が鉄損なので、鉄損値も鉄損分布も精度よく計算できます(Fig.11-3)。
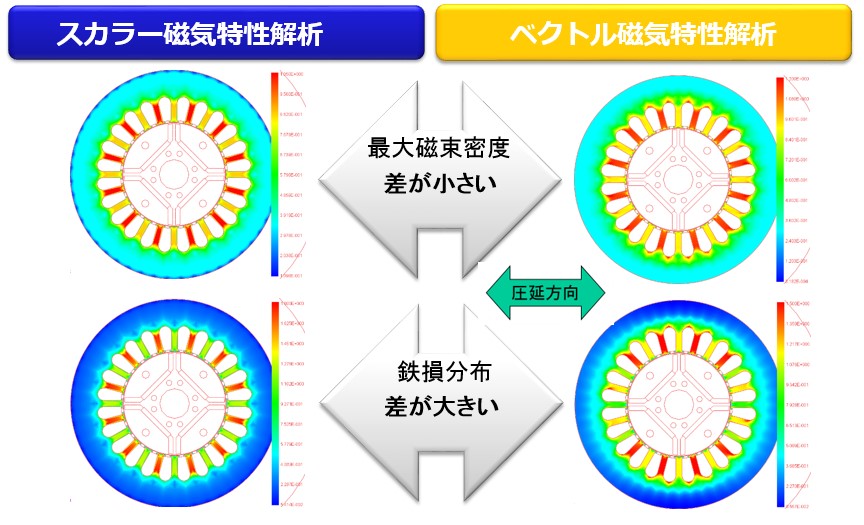
Fig.11-1 従来のスカラ解析法との比較
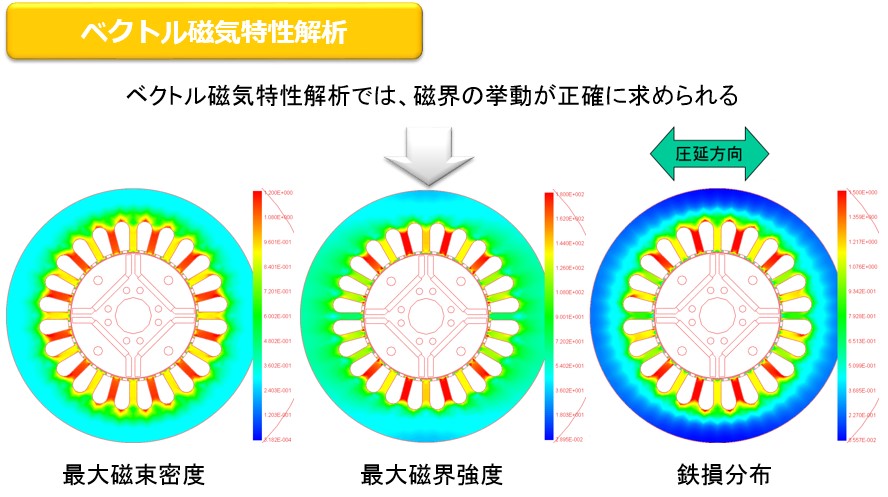
Fig.11-2 精度良い磁界分布
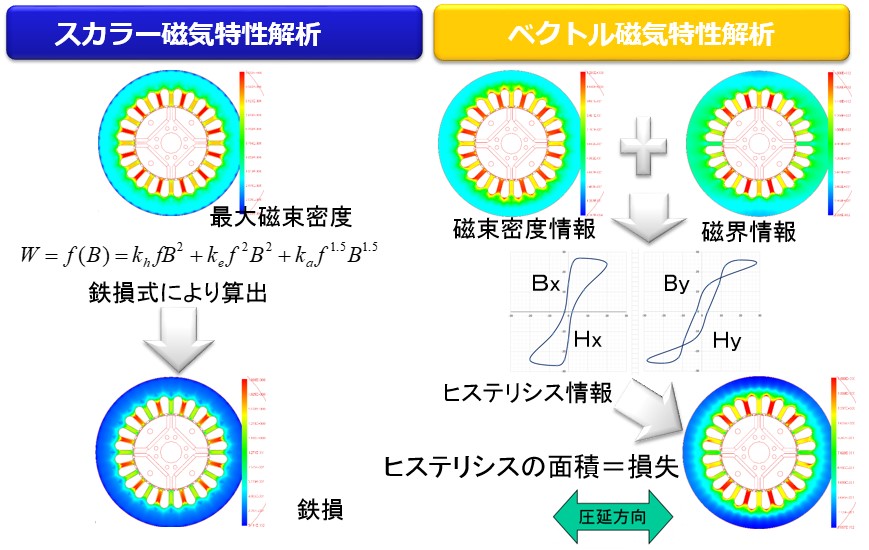
Fig.11-3 精度良い鉄損分布
12.鉄損低減対策
ベクトル磁気特性解析で正確な鉄損分布が分かったら、鉄損が多く発生している場所に対策を施します。例えば、ステータの形状(形やアールとか)を変更してケーススタディ解析を繰り返します(Fig.12-1)。分割コア型(Fig.10)では、圧延方向と磁束方向が一致するように、ステータコアを分割してアセンブルすることにより、鉄損を低減しています(Fig.12-2)。
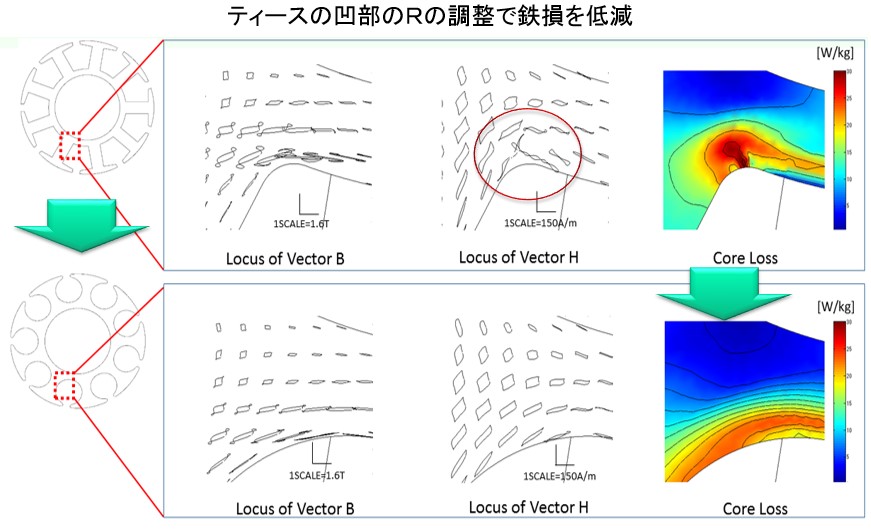
Fig.12-1 鉄損低減対策例
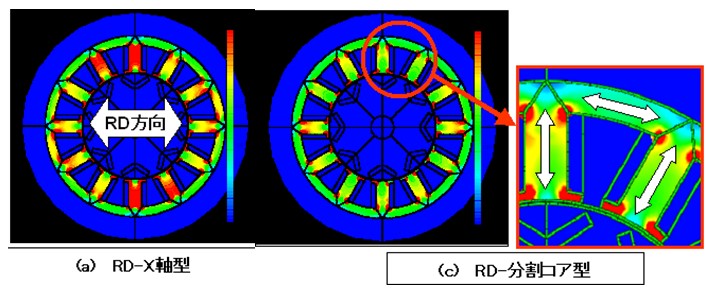
Fig.12-2 分割コア型によるステータの鉄損低減対策
13.鉄損低減対策の手がかりとなるパラメータ
ここで言うパラメータは、ベクトル磁気特性測定に使った軸比α、傾角θB、それに加えてBベクトルとHベクトルの開き各θBHで、それらパラメータと鉄損の関係を示しています(Fig.13-1)。このような傾向が把握出来れば、鉄損低減の方向に各種パラメータが変わるように設計考案する指針とする事が出来ます。各種パラメータの分布をコンター表示する機能も備えています(Fig.13-2)。
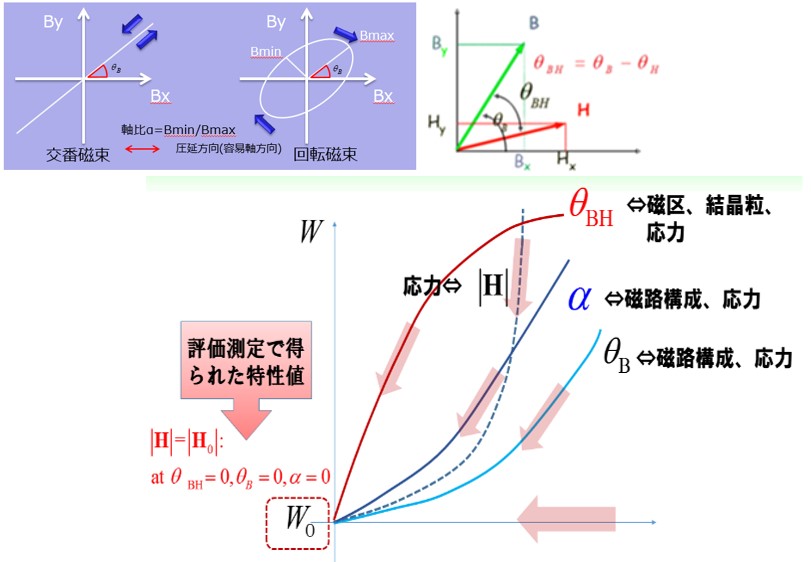
Fig.13-1 パラメータから鉄損低減対策を考案
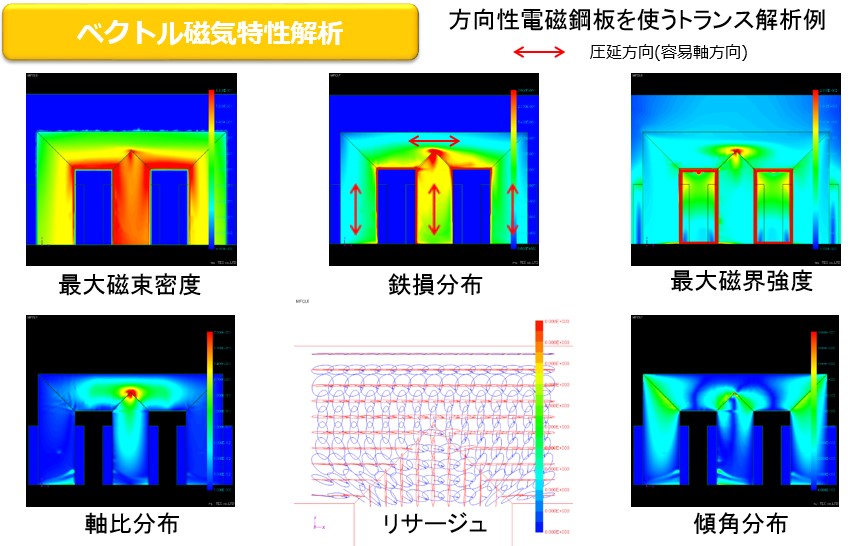
Fig.13-2 パラメータのコンター表示例
14.ダイナミックE&Sモデルへの展開
これまでベクトル磁気特性解析について述べてきましたが、このアルゴリズムはスタティックE&Sモデルというアルゴリズムで構成されています。ベクトル磁気特性測定装置で測定されるのは、磁束密度ベクトルを正弦波励磁した時に発生する、歪んだ磁界強度ベクトル波形になります。しかも測定は50Hzの励磁ですので、50Hzによる渦電流も考慮された波形になります。この磁束密度Bベクトルと磁界強度Hベクトルを使って、x成分Y成分それぞれのヒステリシスカーブが描けます。このヒステリシスカーブは50Hzの渦電流の影響も含んでいますので、ヒステリシスカーブの面積積分は50Hzの鉄損(ヒステリシス損+渦電流損)になります。
そこで課題となるのが、50Hz以外の周波数の時の鉄損です(Fig.14-1)。実機ではもっと高い周波数での利用が考えられます。そしてもう一つの課題が、歪磁束密度波形への対応です。磁束密度は正弦波励磁されているというのがスタティックE&Sモデルですので、歪磁束密度波形の基本波成分を取り出しデータベースを参照していました。この二つの課題に対応するのがダイナミックE&Sモデルです。
ダイナミックE&Sモデルでは、古典的渦電流モデル(薄板中の渦電流をモデル化)を使って、使用周波数の渦電流による磁界強度を算出し補正します。また歪磁束密度に対しては、高調波成分に分解しその周波成分における渦電流の影響を算出し補正します。こうしてより実際に近いベクトル磁気特性関係をシミュレーションできるようになります。
ダイナミックE&Sモデルは、μ―E&Sのグレードアップとして近々組み込んで行きます。
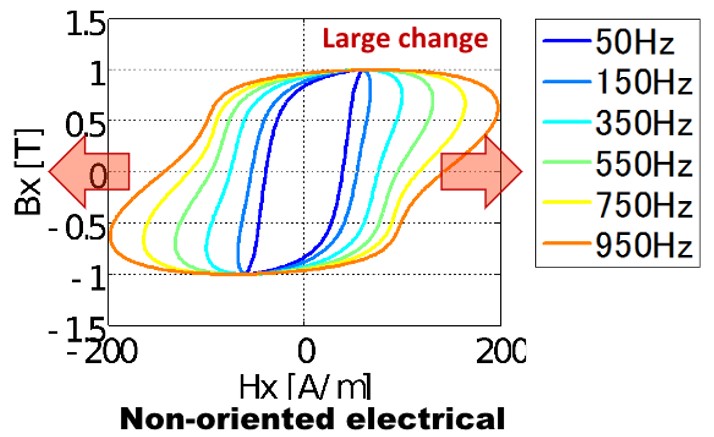
Fig.14-1 ヒステリシスカーブの周波数依存性
15.応力の影響を考慮
榎園教授を中心としたベクトル磁気特性技術の研究では、既に応力の影響に対しての発表が数多くなされています。詳細は「ベクトル磁気特性技術研究所」のホームページをご参照ください。μ-E&Sへの機能実装はまだ先の話になります。
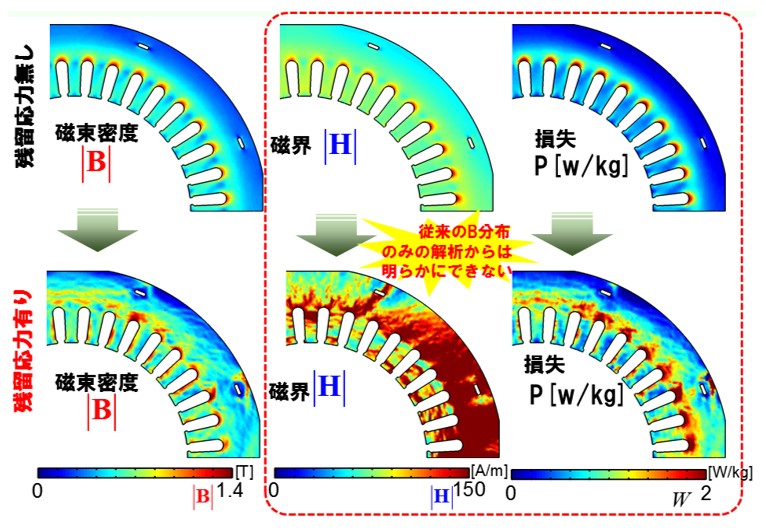
Fig.15-1 残留応力を考慮した鉄損解析
16.μ-E&Sの機能表
| 解析種類 | 2次元非定常磁場解析(FEM) |
|---|---|
| アルゴリズム | E&Sモデル |
| 励磁 | 電圧源、電流源、永久磁石 |
| 材料データベース | 方向性・無方向性電磁鋼板 4種 |
| 対象モータ | 同期モータ(誘導モータは開発中) |
| モデル入力 | FemapNEUファイル(別途 自社メッシャ―付属) |
| 出力(数値、図) | 磁束密度・磁界ベクトルの時間変化、ヒステリシスループ、鉄損、電流波形、最大磁束密度、最大磁界強度、傾角、軸比、トルク |
| GUI | ウィザード方式の使いやすいインターフェース装備 |
Fig.16-1 μ-E&Sのインターフェース


