解析事例集(1)リングモデル 電圧源
目次
1.解析モデルと目的
解析モデル図をFig1.1.1に示す。解析モデルは無方向性電磁鋼板(50A470)をリング状に打ち出したモデルを想定。励磁コイルに電圧を入力し、最大磁束密度が1.6T程度になるように励磁。電磁鋼板の圧延方向はX方向としている。このモデルは、電磁鋼板が無方向性であっても、圧延方向に対する磁気異方性がある事を確認する解析モデルになる。また、どの部分も交番磁束になるモデルだが、ベクトル磁気特性測定では回転磁界が見られるので、それが計算できることも確認する。
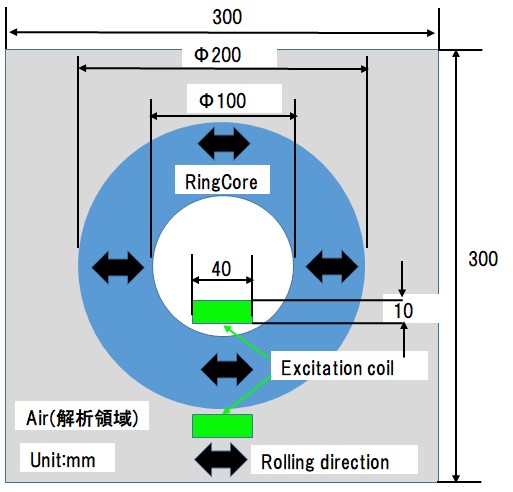
Fig.1.1.1 モデル図
2.解析条件と計算時間
解析に使用したメッシュモデルをFig1.2.1に、解析条件をFig.1.2.2に示す。電圧条件は、最大磁束密度が1.6T程度になるように設定(尚、電流入力で計算する場合は,コイルの総電流量が大体35(Aturn)くらいになる)。計算時間は約8min(IntelCorei5,28GHzマシン)、非線形のイタレーションが216回で収束した。

Fig.1.2.1 メッシュモデル
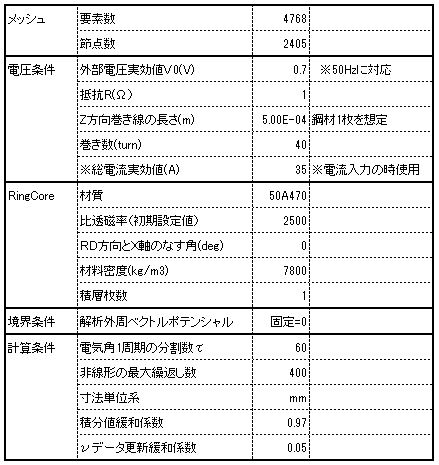
Fig.1.2.2 解析条件
3.磁場分布、鉄損分布結果
最大磁束密度分布、最大磁界強度分布、鉄損分布をFig1.3.1、Fig1.3.2、Fig1.3.3に示す。磁束密度分布では、圧延方向と磁束密度ベクトルが平行(傾角θB=0)の上下領域で磁束密度が最大になり、左右領域程に磁束密度が一様化している。これは圧延方向の磁気抵抗が小さい上下領域で、さらに磁路長の短い内径側に磁束密度が集中したものである。逆に磁界強度分布は、磁束密度ベクトルが圧延方向と直角な左右領域で磁気抵抗が大きい=磁界強度が大きい傾向になっている。鉄損分布では、磁束密度の大きい上下領域で鉄損も大きい傾向だが、磁束密度分布に比べて左右領域でも大きい、これは鉄損が磁束密度と磁界強度のスカラー積で、磁界強度の大きい左右領域の影響を受けたものである。このように、従来の計算法では鉄損分布は磁束密度分布と同じ傾向を示していたが、ベクトル磁気特性解析では正確な磁界強度とその影響も考慮した鉄損分布を計算できる事を示している。
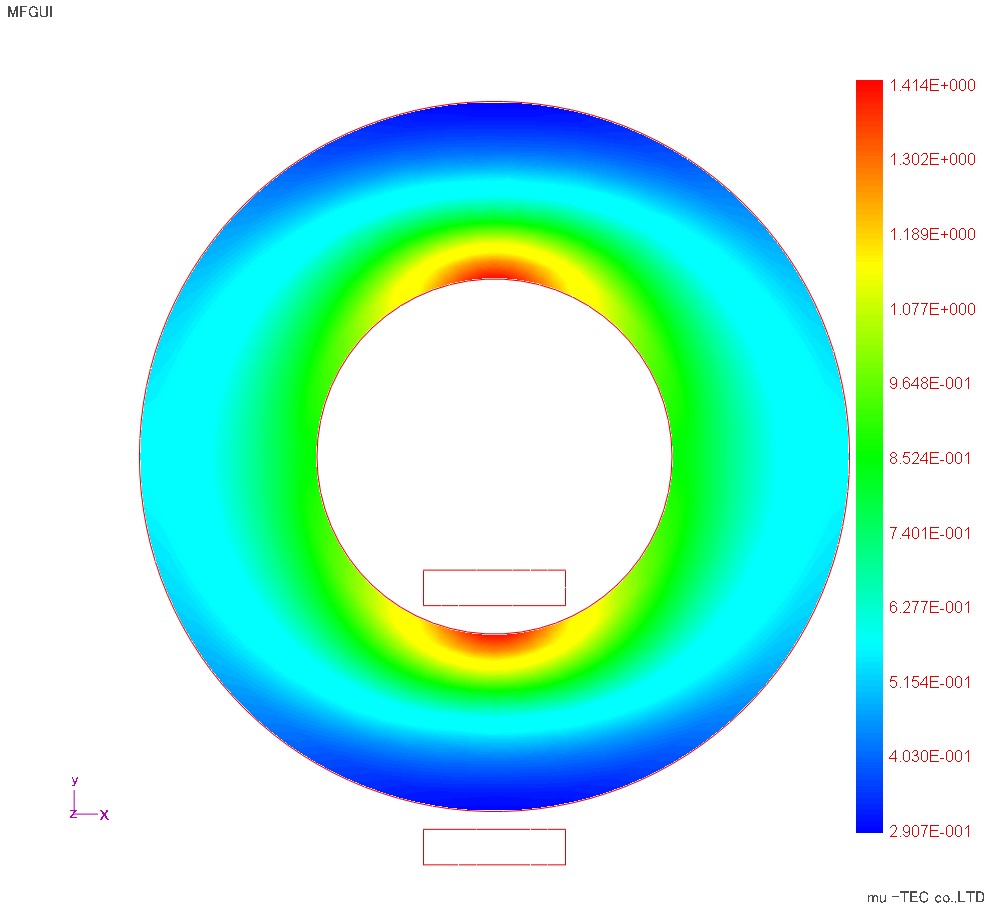
Fig.1.3.1 最大磁束密度分布(最大1.41Tで表示)
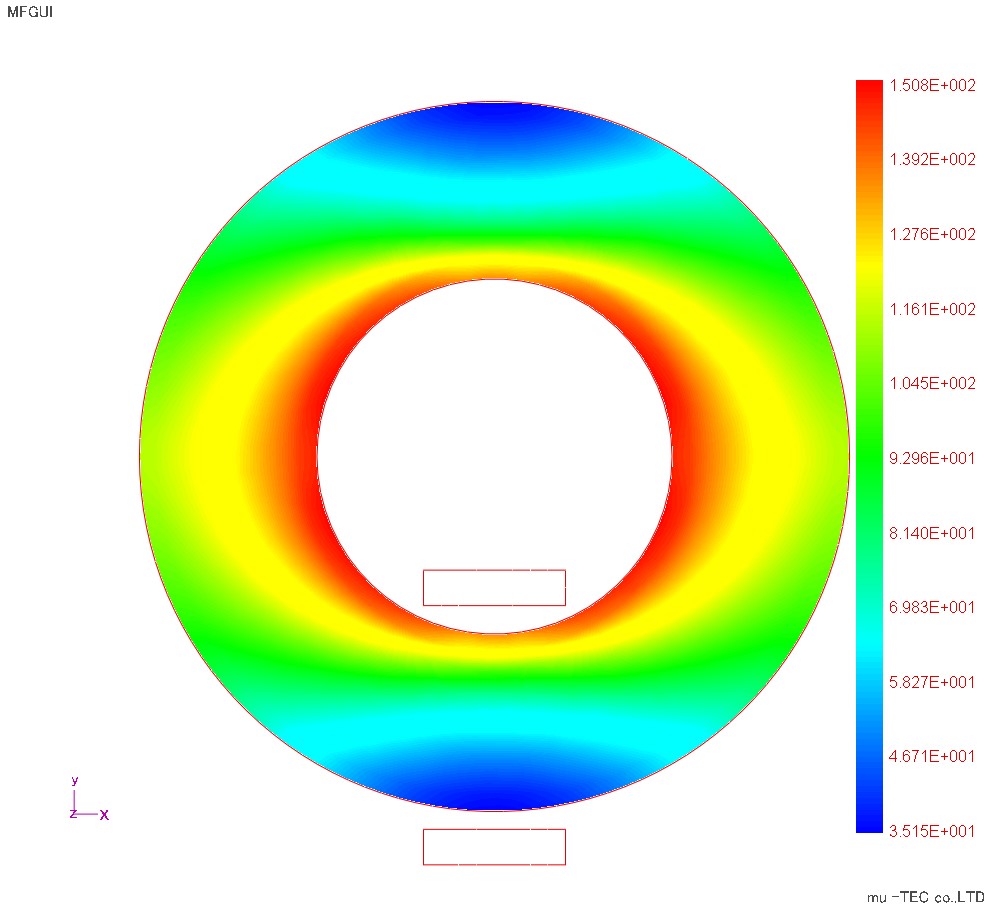
Fig.1.3.2 最大磁界強度分布(最大150A/mで表示)
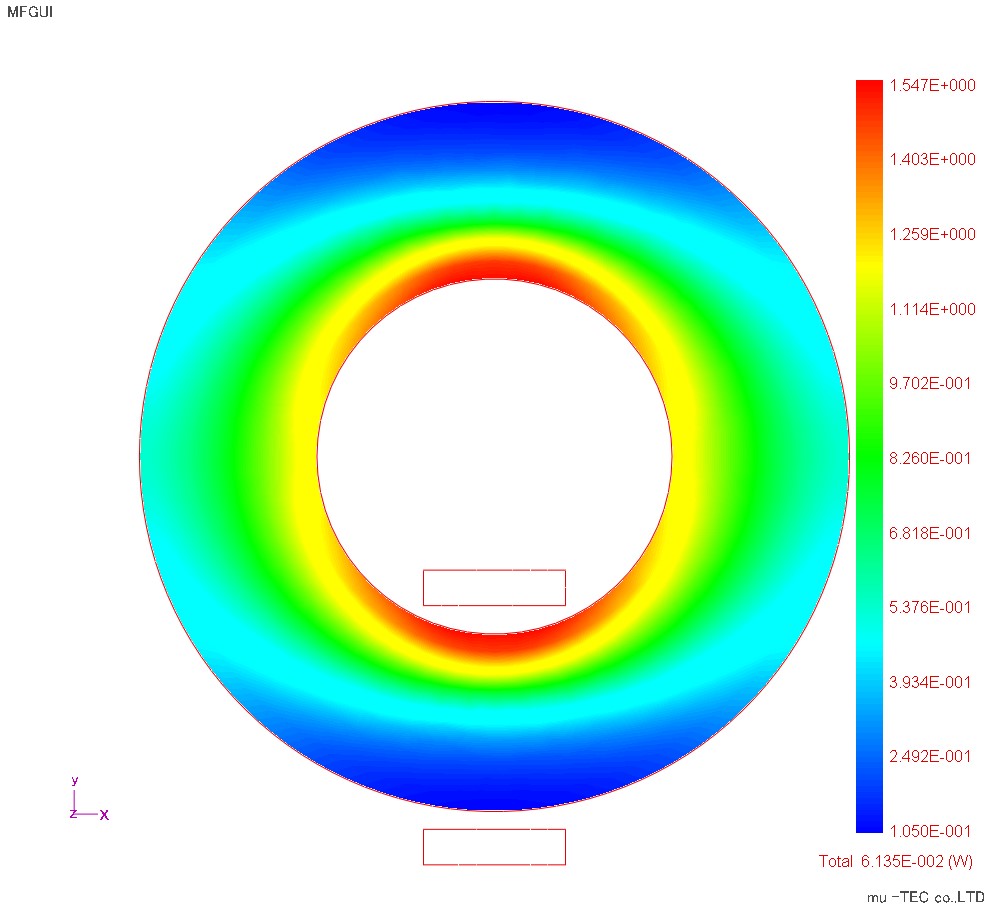
Fig.1.3.3 鉄損分布(最大1.5W/kgで表示)(モデルで考慮した積層1枚の総鉄損値は0.135e-2(W))
4.交番磁束と回転磁界結果
Fig1.4.1は磁束密度ベクトル(赤)と磁界強度ベクトル(青)のリサージュ波形を正規化(波形を同じ大きさで表示)した図である。赤い磁束密度ベクトルのリサージュ波形は、交番磁束(回転磁束ではない)で、同心円状に綺麗に向きが変化している。尚、Fig1.4.2は正規化していない表示で、外径側に行くほどリサージュ波形が小さくなっている事が確認できる。さらにFig1.4.1の丸印(角度45度方向のある位置)のリサージュ波形の拡大図がFig1.4.3である。この図では磁束密度ベクトル(紫)は135度方向の交番磁束であるが、磁界強度ベクトル(緑)は傾きが120度方向で回転磁界になっている。この結果もベクトル磁気特性測定結果らえられた計算結果である。
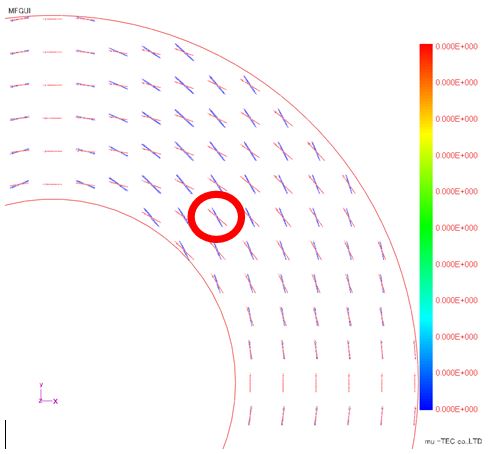
Fig.1.4.1 リサージュ波形(正規化)
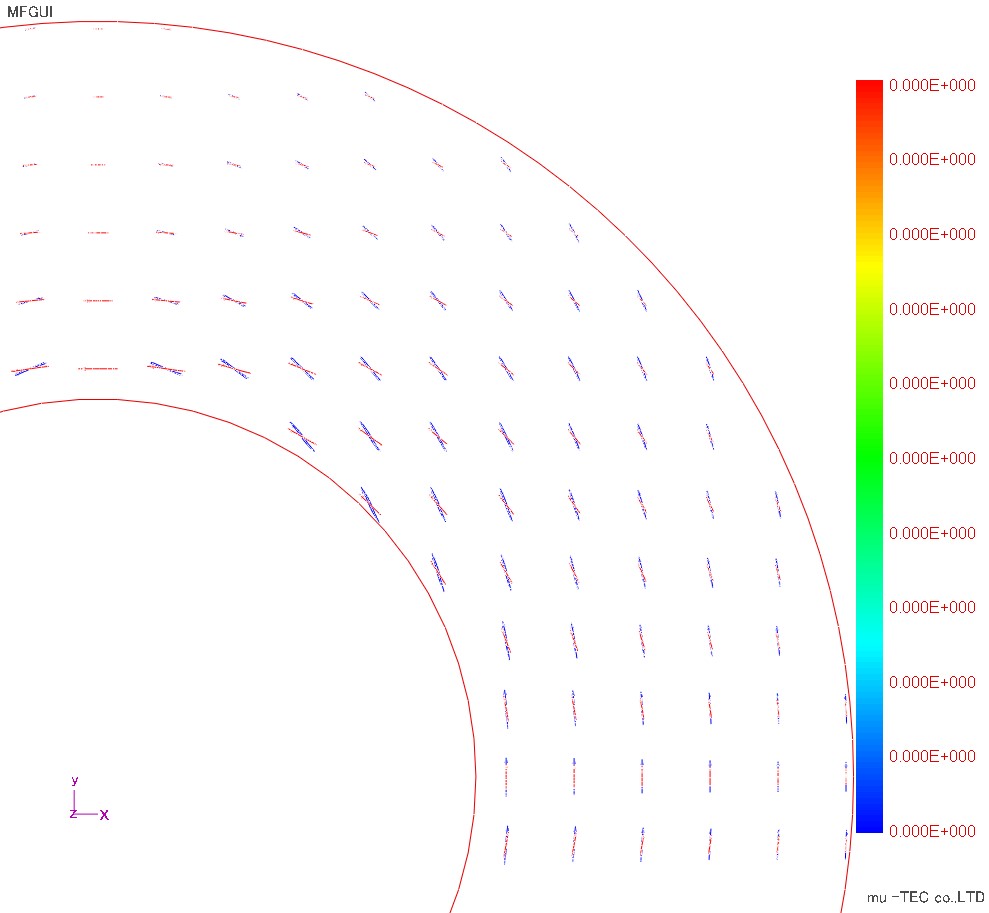
Fig.1.4.2 リサージュ波形(正規化無)
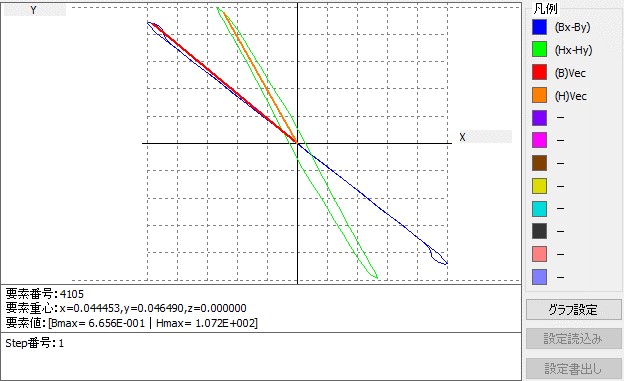
Fig.1.4.3 リサージュ波形の拡大表示(紫:磁束密度、緑:磁界強度)
5.ヒステリシスカーブの測定値との比較結果
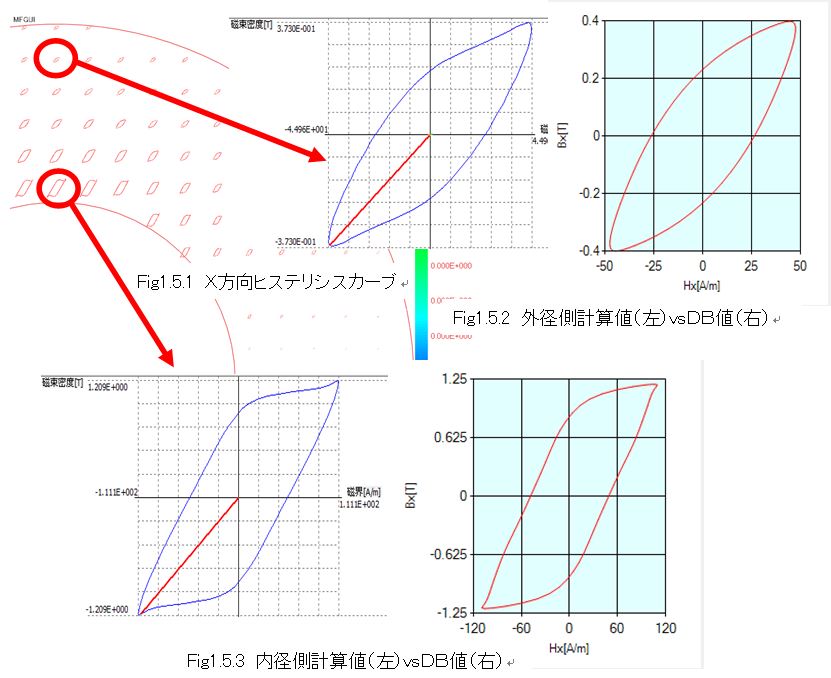
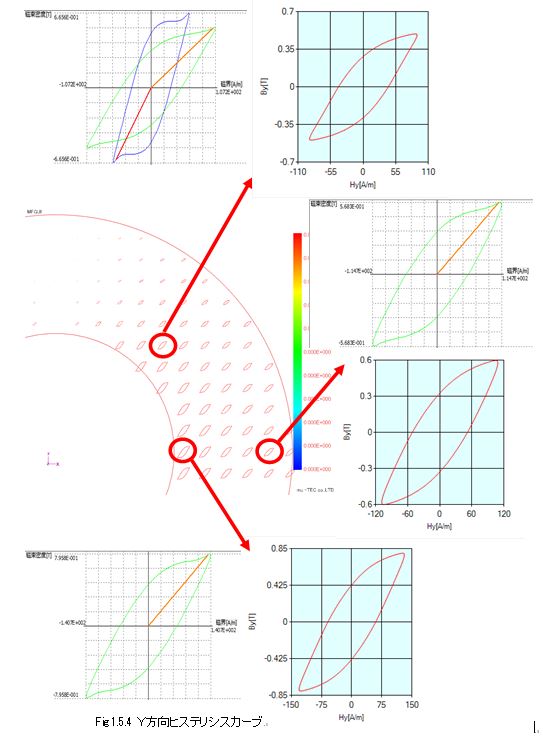
Fig1.5.1にX方向ヒステリシスカーブ(HxとBxによるカーブ)の分布を示す。丸印はリング試料の0時方向の場所で、交番磁束がX方向のみになる場所である。磁束密度の小さいリング試料外径側のヒステリシスをFig1.5.2に示す。左側が計算値で、最大磁束密度0.37T,最大磁界強度45A/m、これに対応するDB(データベース内の)値を右側に示したが良く一致している。参照したDB値は最大磁束密度Bmax=0.4T、交番磁束の圧延方向からの傾角θB=0、交番磁束を表す軸比α=0の波形である。DB値は、この条件における測定値そのものである為、得られた計算結果は測定値と良く一致していると考えることが出来る。ベクトル磁気特性解析のE&Sアルゴリズムは、測定波形のデータベースを材料特性として、有限要素法の磁場解析を行うものであるので、計算結果はデータベースの波形に一致し、それは測定値と精度よく一致するという事が言える。同様に磁束密度の大きいリング試料内径側のヒステリシスをFig1.5.3に示したが、こちらも計算結果とDB値は良く一致している。Fig1.5.4ではY方向ヒステリシスカーブについて、各場所の計算結果とDB値を比較して、一致性を確認した。
6.電流波形結果
励磁方法は電圧源と電流源で与えられるが、今回電圧源方式にしたので結果として電流波形が得られる(Fig1.6.1)。最大電流値は約1Aで、40ターンの条件なので総電流量は約40Aturnになる。波形ではCOS波と比較しているが、得られた電流値は歪んでいる事がわかる。例えば、もっと磁束密度が大きくなると飽和して磁気抵抗が大きくなるので、波形ピークが尖った3角波に近くなる。このように磁気特性の非線形性が考慮できるので、電圧源方式の計算が望ましい。
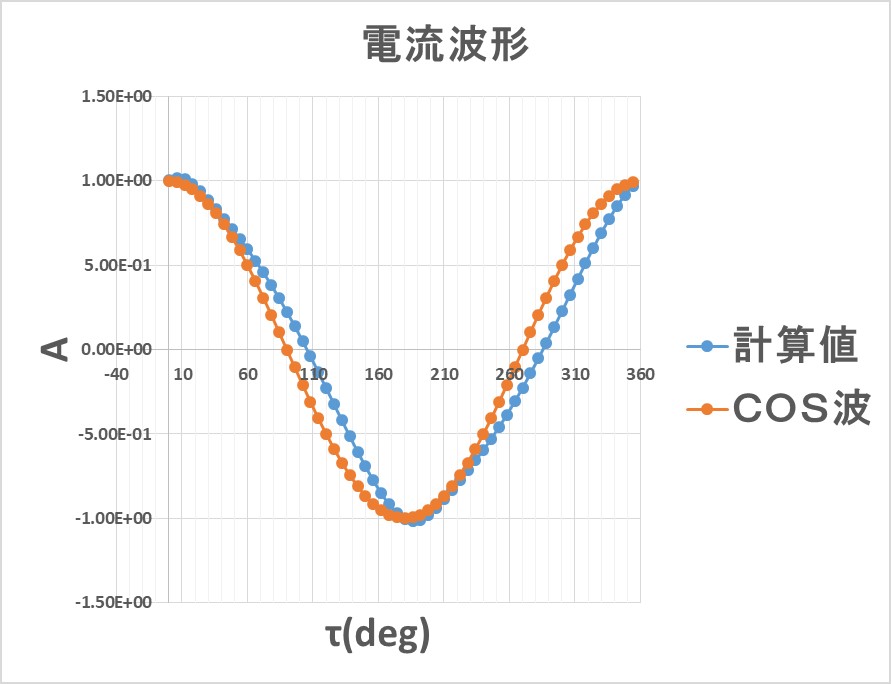
Fig.1.6.1 電流波形
7.インターフェース設定画面
ここではμ-E&Sの操作手順を、インターフェース画面順に紹介する。

Fig.1.7.1 μ-E&Sの起動
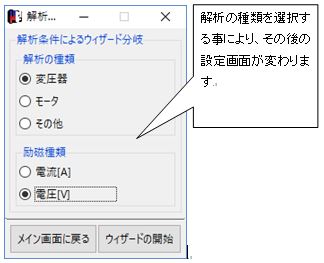
Fig.1.7.2 解析ウィザードによる解析種類の選択
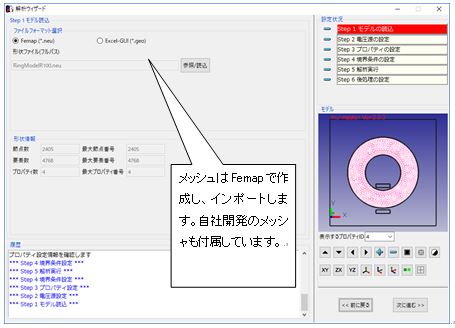
Fig.1.7.3 Femapで作成したリングモデルのインポート
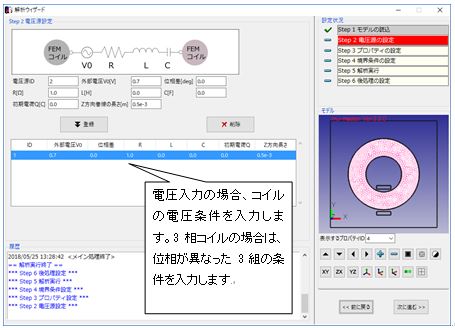
Fig.1.7.4 電圧条件の設定
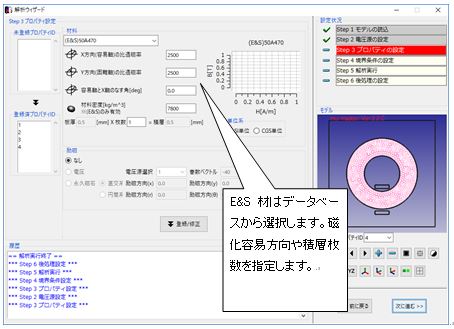
Fig.1.7.5 材料の設定
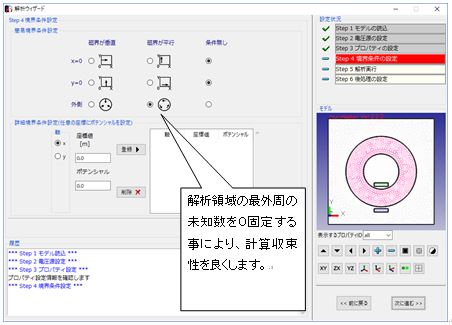
Fig.1.7.6 境界条件の設定
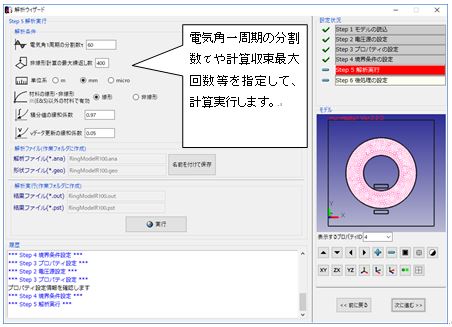
Fig.1.7.7 収束回数等の解析条件設定と計算実行
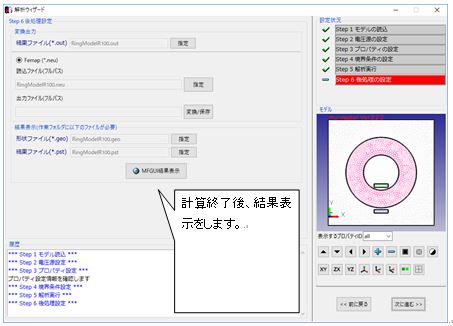
Fig.1.7.8 結果表示の準備
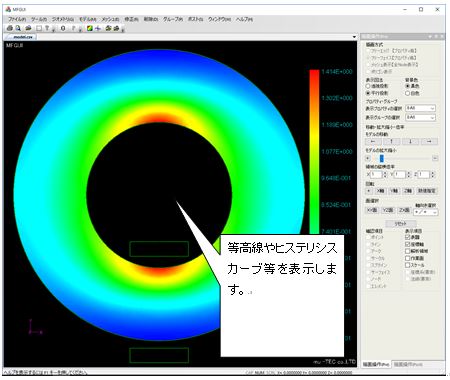
Fig.1.7.9 結果表示
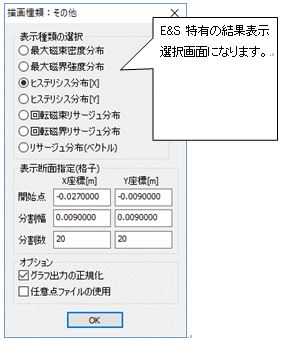
Fig.1.7.10 ヒステリシスやリサージュ波形の設定


