解析事例集(8)誘導モータ モデルI
目次
1.解析モデルと目的
電気学会検証問題 誘導モータモデルIの基本解析を行う。ステータ配線図、ロータ2次導体回路図をFig8.1.1、Fig8.1.2に示す。このモデルは電気学会の回転機:調査専門委員会ベンチマーク問題の一つ、番号R8,Iモデル(かご型誘導電動機)(技法:第776号4章)を参照している(但し、技法には詳細な条件の明記が無いため、推定値も設定している)。誘導モータでは回転時すべりが発生し、ステータコアからの回転磁界とロータコアの回転が同期していない為、ベクトル磁気特性解析で回転時の解析は出来ない。そのためロータコアを固定した状態の、始動時の解析を想定し、ベクトル磁気特性解析を行った。ステータコアとロータコアには回転磁束が発生する為、無方向性電磁鋼板50A470でX方向を圧延方向に指定し、ベクトル磁気特性解析を適用する領域となる。ステータ側の励磁コイルに電圧を入力し、ロータ側の2次導体(bar)には、電圧0の回路を設定し、2次導体の電流を算出した。また、始動時トルクを算出した。
ステータ側の配線は以下(Fig8.1.1)のようにした。解析ではU,V,Wの回路と連成させて解く。U,V,Wそれぞれの回路には電圧番号(今回は1,2,3)をがあり、外部電圧V0、巻き線抵抗R、位相を設定(Fig.8.2.1)する。例えば+Uコイルのプロパティ番号を4とすると、電圧番号1とリンクする。さらに1スロット当たり60巻きターンなので、+Uコイル4つで240巻きターンと指定する。また、-Uコイルも電圧番号1とリンクするが、巻きターンは-240と指定する。この巻きターンの事を巻き数ベクトルと呼んでいるが、電流の向きも指定していることになる。計算では、電圧番号1が指定されている節点のベクトルポテンシャル(Az)を全て積算することにより、電圧番号1に鎖交する磁束量を算出している。あとは巻きターン数と積層鋼板の積み厚さを指定して時間微分することで、電圧番号1の誘起電圧を算出して回路方程式を解き、得られた電流値が有限要素法の励磁電流値になるという仕組みである。これらの操作は、有限要素法の方程式と連立して同時に解いている。
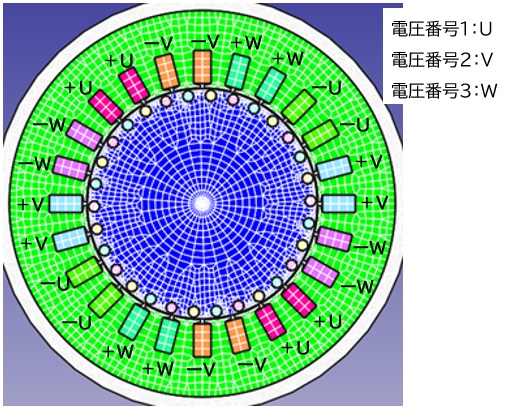
Fig.8.1.1 励磁巻き線条件
ロータ側の2次導体に関しても、今回は回路方程式を利用した。Fig8.1.2に示したのが2次導体とリンクする電圧番号である。電圧番号それぞれの外部電圧は0Volt、位相は0、抵抗をFig8.2.1に示す。2次導体は銅やアルミのbarなので、巻きターン数は1導体当たり1である。設定では2つの2次導体が同じ電圧番号にリンクされているので、巻き数ベクトルは2になる。ただし、巻き数ベクトルがマイナスになる対が存在しない為、巻き数ベクトルを4にして、鎖交磁束を算出している。
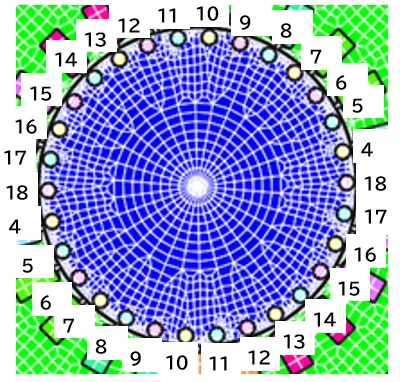
Fig.8.1.2 2次導体の電圧番号
2.解析条件と計算時間
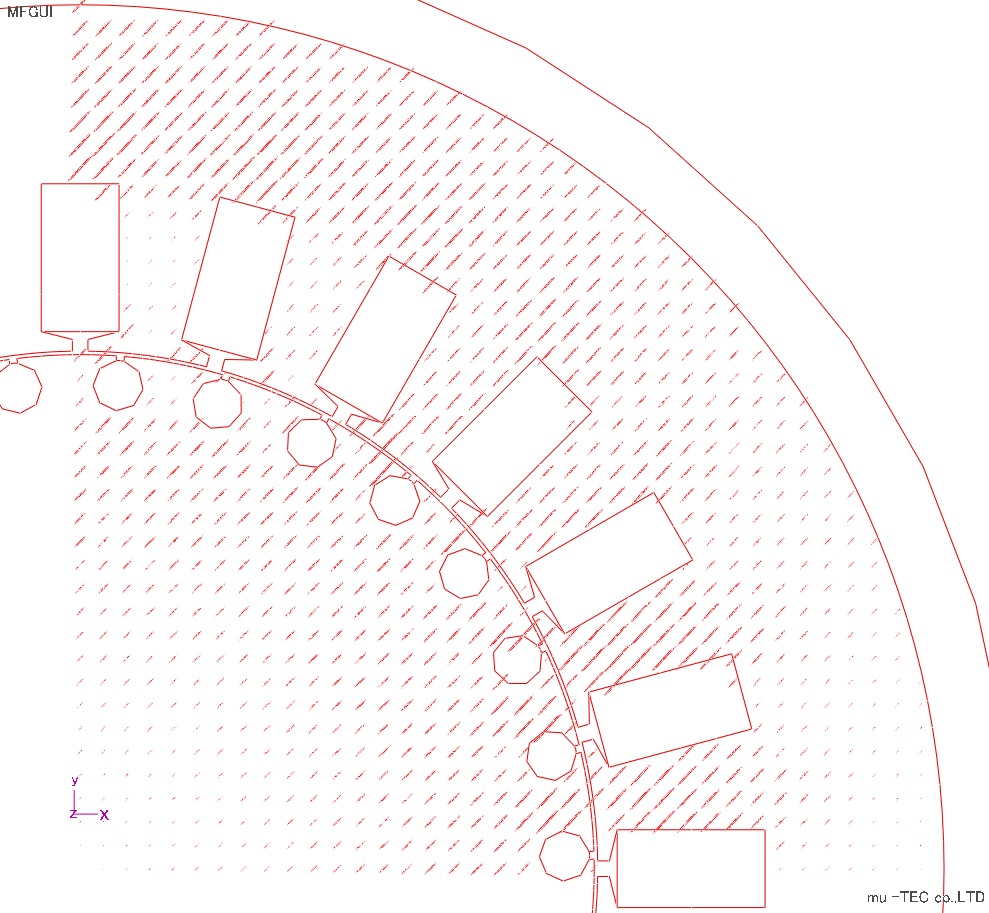
技法よりこのモータは4極ー200Voltー50Hzで、その解析条件をFig.8.2.1に示す。計算時間は約180min(IntelCorei5,28GHzマシン)、非線形のイタレーションが40回(Fig8.2.2)。メッシュ図をFig8.2.3に示す。
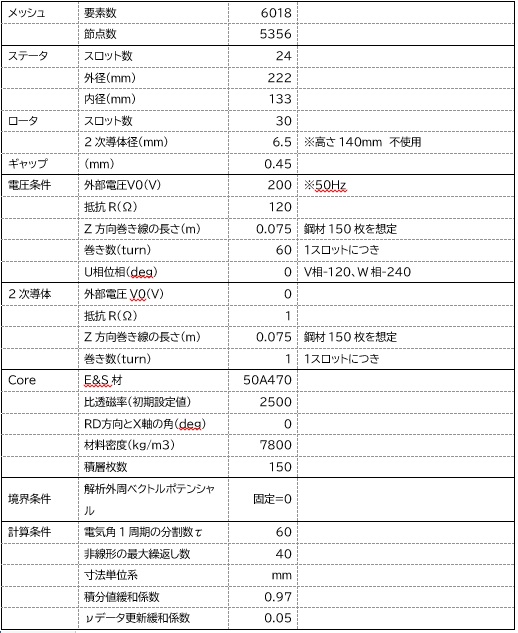
Fig.8.2.1 解析条件

Fig.8.2.2 計算時間と収束回数
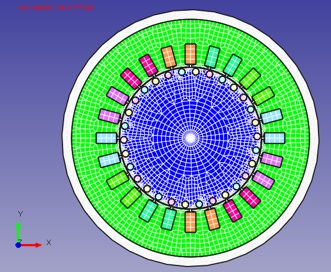
Fig.8.2.3 メッシュ図
Fig.8.2.4 リサージュ波形の評価点
3.磁束線、磁場分布、鉄損分布結果
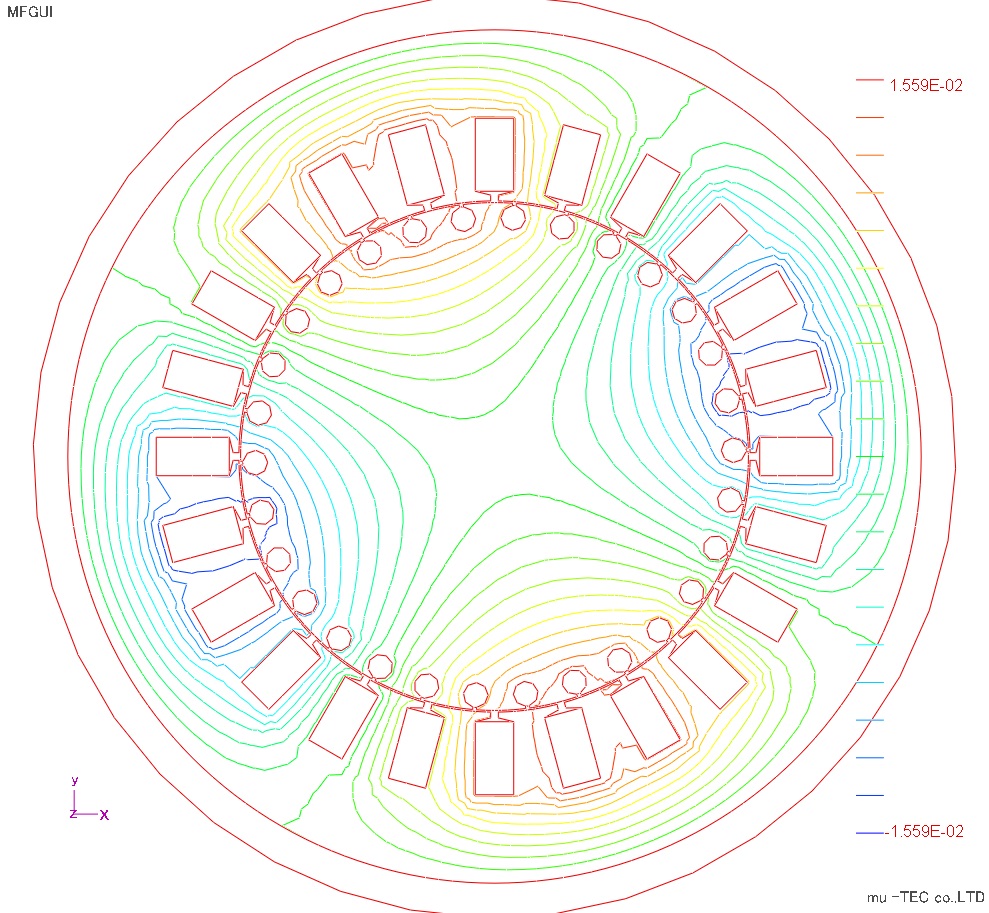
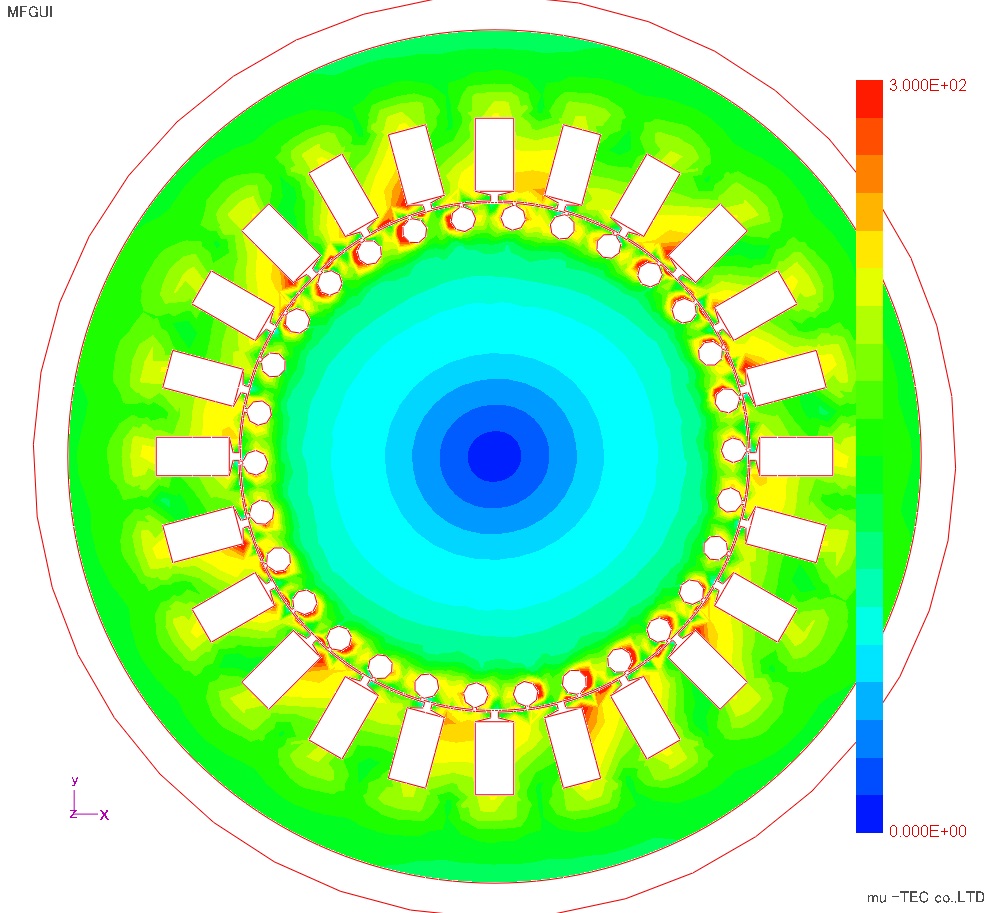
磁束線図、最大磁束密度分布、最大磁界強度分布、鉄損分布をFig8.3.1からFig8.3.4に示す。磁束密度はティース先端部分および2次導体周辺が大きくなっているが、周方向にはほぼ同程度になっている。磁界強度は上下領域のティース部分および2次導体周辺でが大きく、圧延方向がX方向による影響が出ている。鉄損分布は、磁界強度の影響を受けて上下領域のティース部が若干大きくなっている。従来の鉄損式を使った方法では、磁束密度分布と同様に周方向に変化は見れないので、ベクトル磁気特性解析の効果を確認出来る。
 |
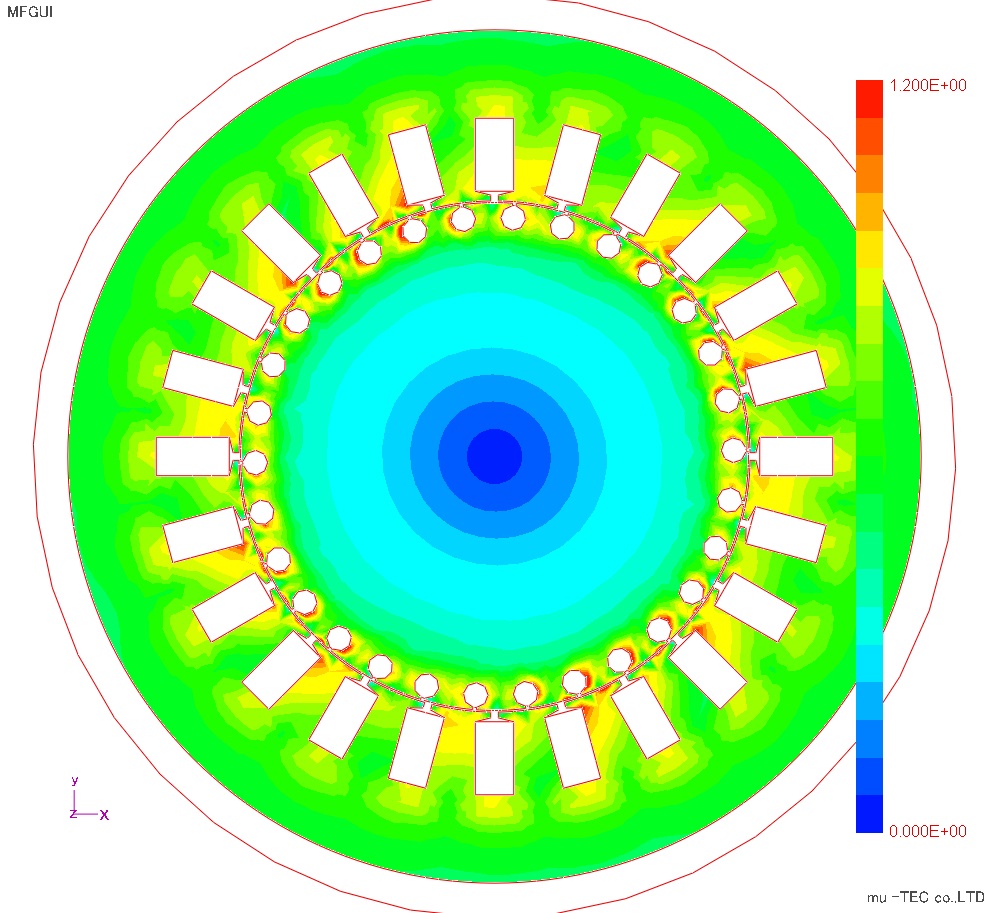 |
Fig.8.3.1 磁束線図 |
Fig.8.3.2 最大磁束密度分布(最大1.2Tで表示) |
 |
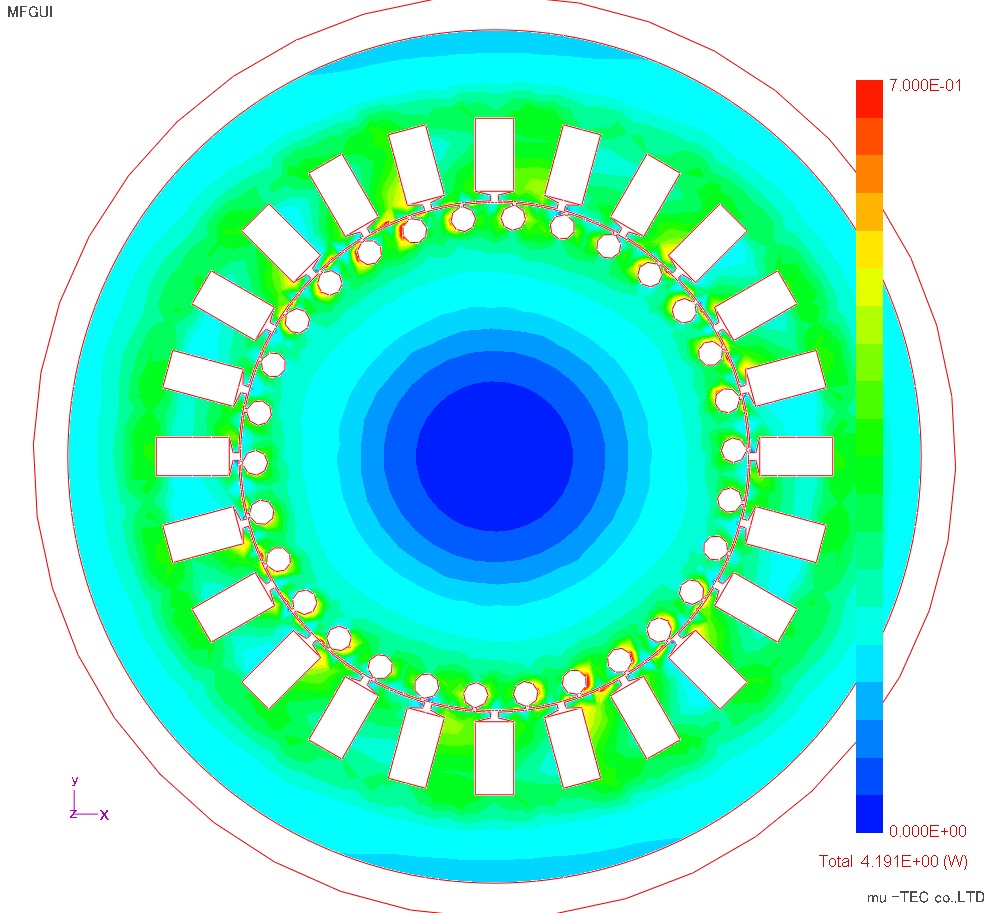 |
Fig.8.3.3 最大磁界強度分布(最大300A/mで表示) |
Fig.8.3.4 鉄損分布(最大0.7W/kgで表示) |
4.傾角θBと軸比α分布結果
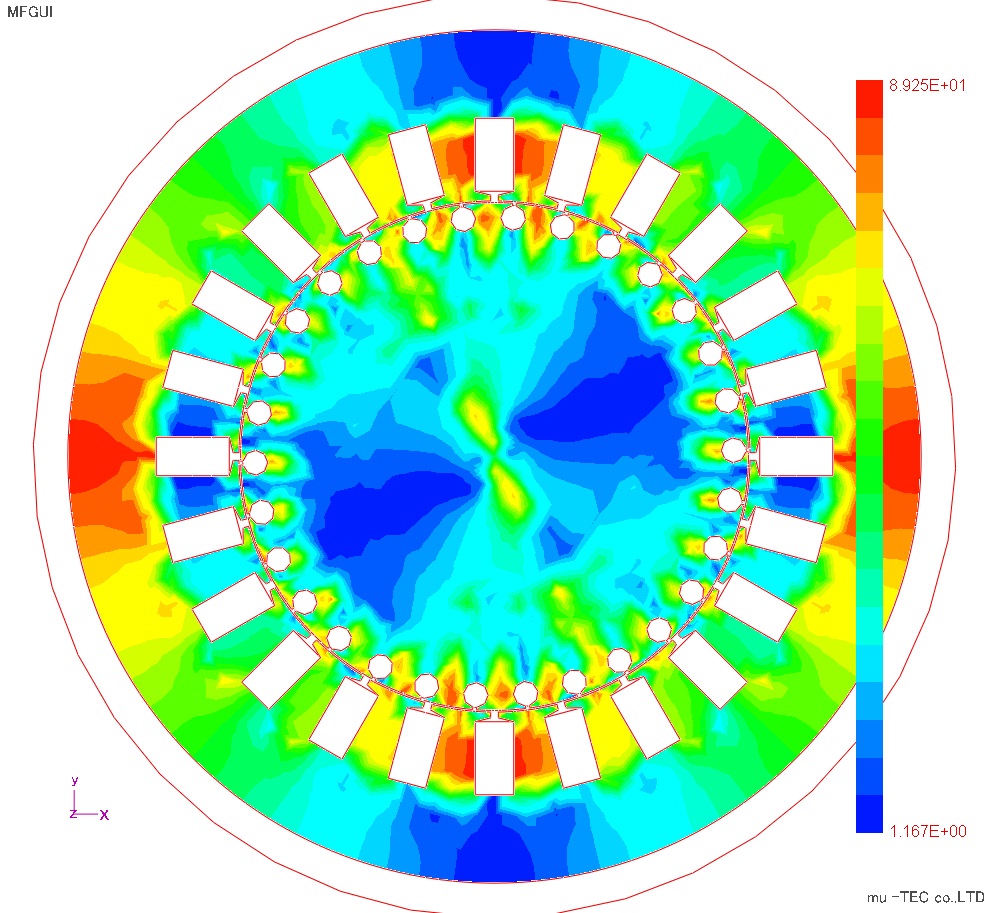
傾角θbは圧延方向に対する交番磁束の反時計回りの角度で、回転磁束の場合は最大磁束密度の方向との角度である。傾角θB分布結果をFig8.4.1に示す。傾角θBは上下ティース部および左右ティース部付け根付近で大きくなっている、これは磁束の流れと圧延方向の関係で理解できる。最大角度は約90度になっている。軸比αは回転磁束の長軸と短軸の比で、α=1は真円、α=0は交番磁束である。軸比α分布結果をFig8.4.2に示す。軸比αの最大は各ティース部の付け根と2次導体内径側が大きい、特にロータ軸付近は完全な回転磁束となっていて妥当である。
 |
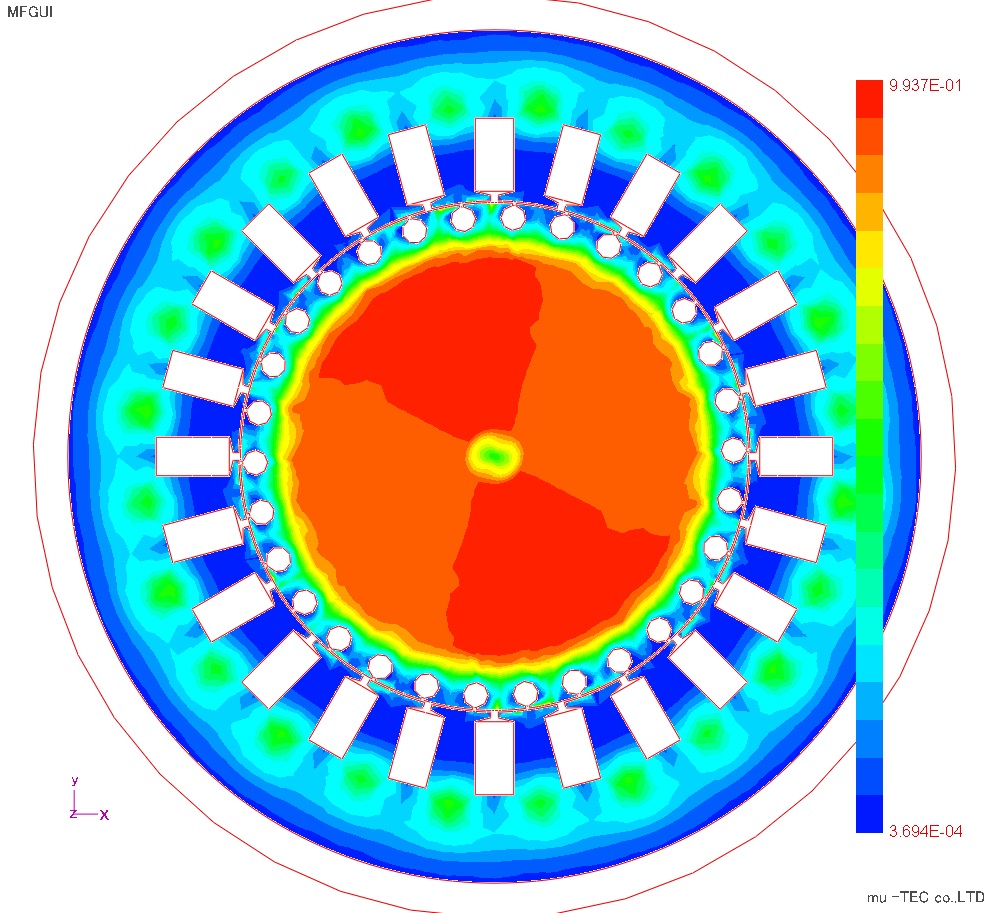 |
Fig.8.4.1 傾角θB 最大89.2度 |
Fig.8.4.2 軸比α 最大0.99 |
5.ヒステリシスカーブ結果
ヒステリシスカーブの分布結果(正規化なし)をFig8.5.1、Fig8.5.2に示す。
 |
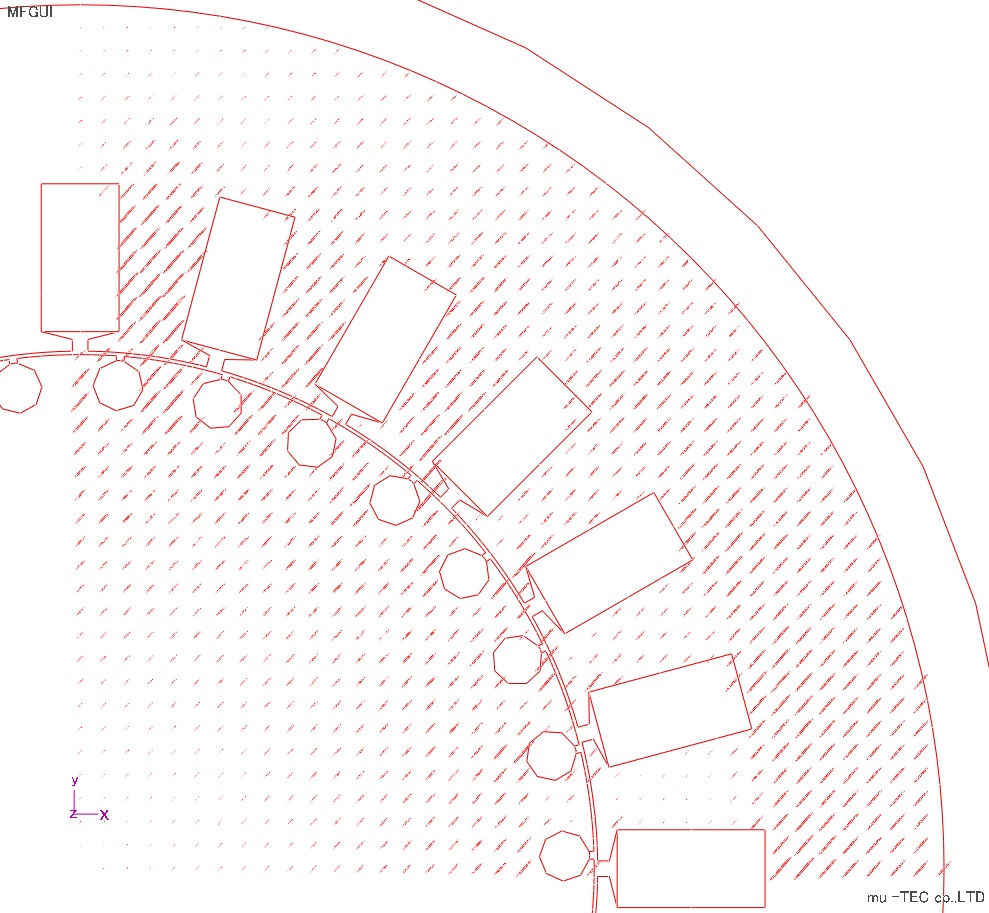 |
Fig.8.5.1 X方向ヒスカーブ(正規化なし) |
Fig.8.5.2 Y方向ヒスカーブ(正規化なし) |
6.リサージュ波形結果
磁束密度及び磁界強度のリサージュ波形(正規化有り、無し)をFig8.5.3、Fig8.5.4に示す。磁束密度ベクトル(赤)は、磁界強度ベクトル(青)で表示している。※赤:磁束密度ベクトル、青:磁界強度ベクトル
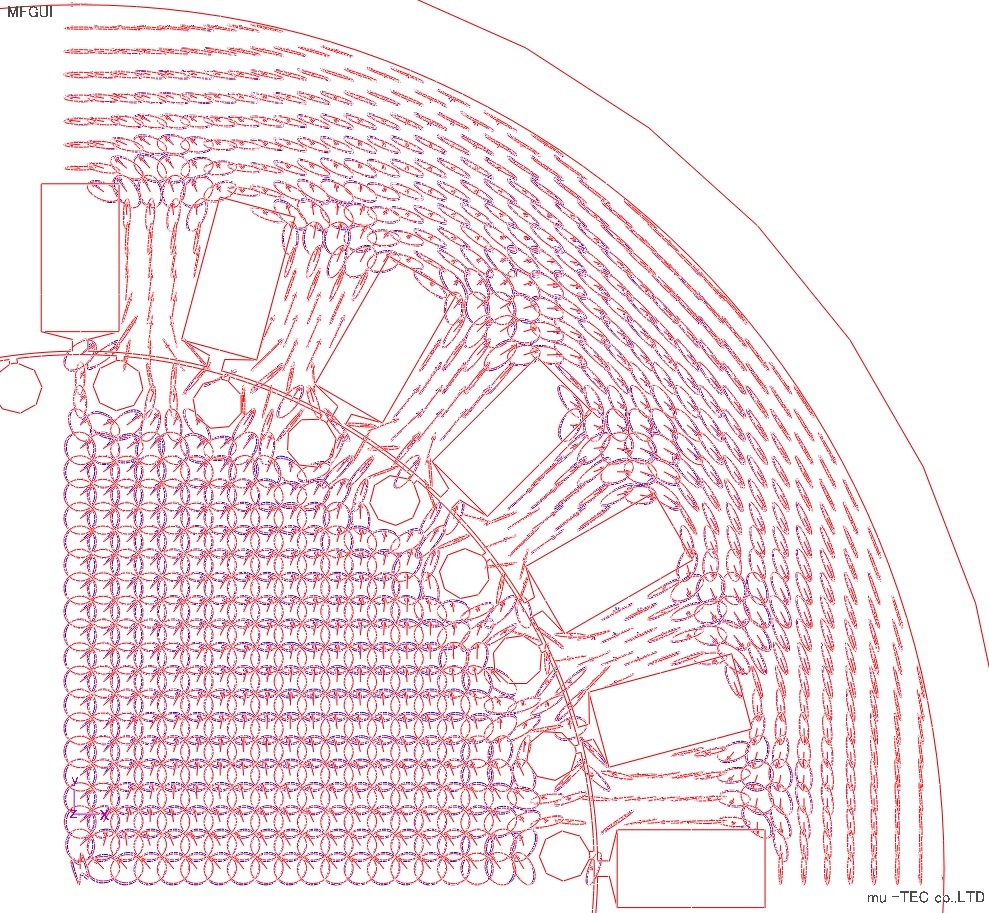 |
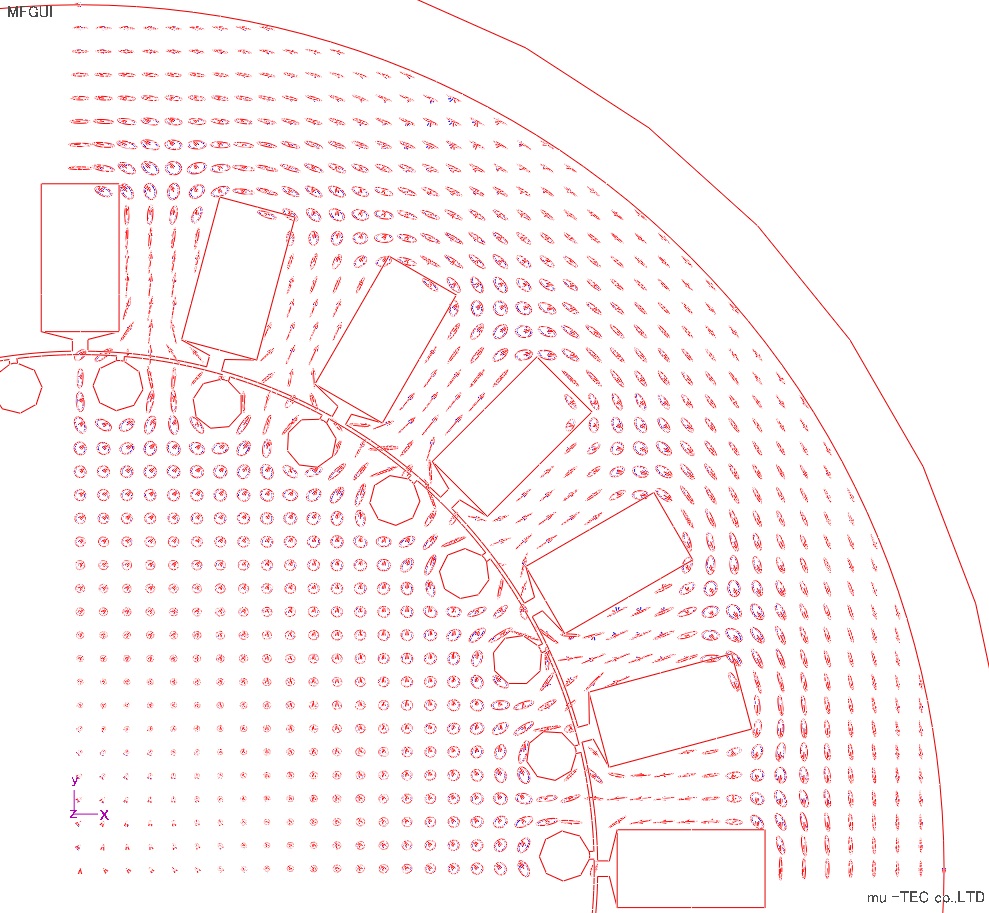 |
Fig.8.5.3 リサージュ波形(正規化有り) |
Fig.8.5.4 リサージュ波形(正規化なし) |
7.電流波形とトルク波形結果
電流波形をFig8.7.1に示す。三相なのでU,V,Wの波形を示している。電流ピーク値は1.7A程度。2次導体の電流ピーク値は1.5A程度。始動時トルク変動は、平均で20Nm/m程度で、技法の結果と同程度であった。
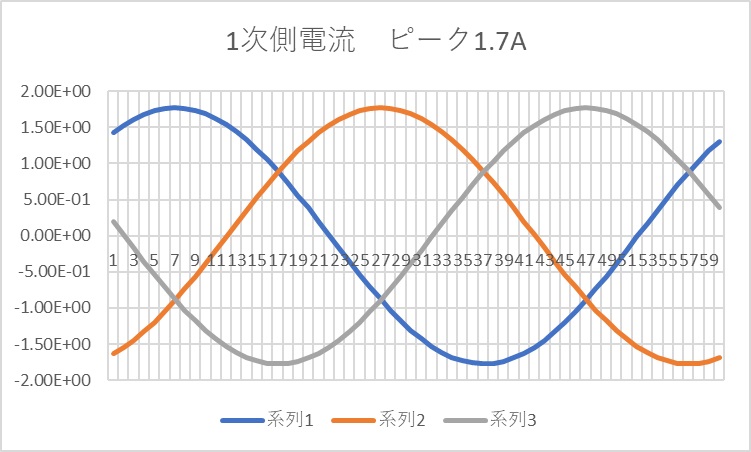
Fig.8.7.1 1次側電流波形
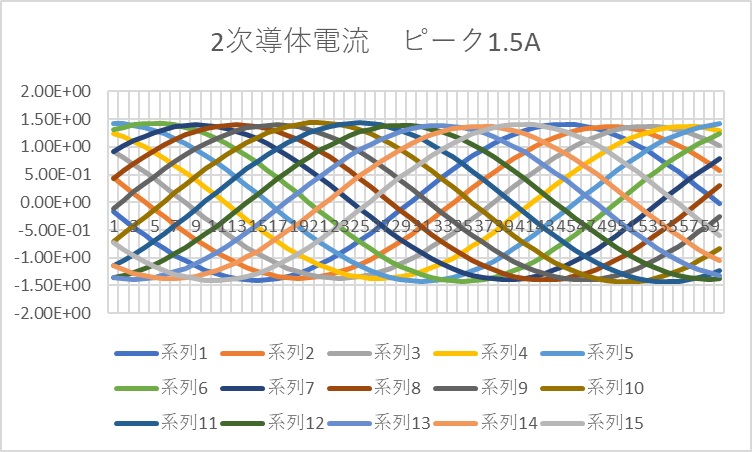
Fig.8.7.2 2次側電流波形
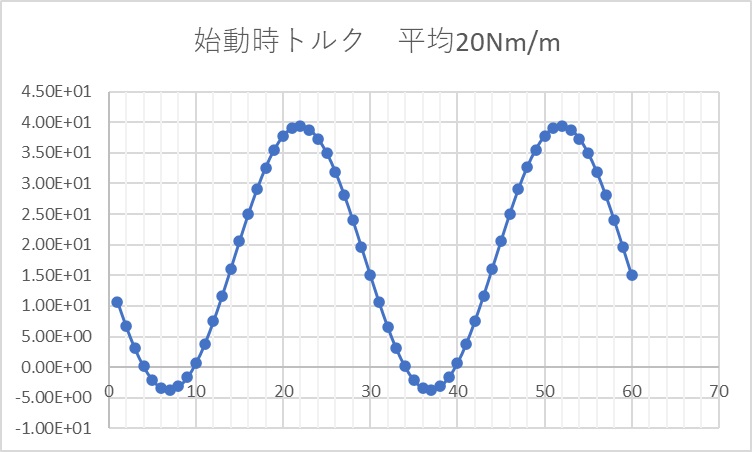
Fig.8.7.3 始動時トルク変動
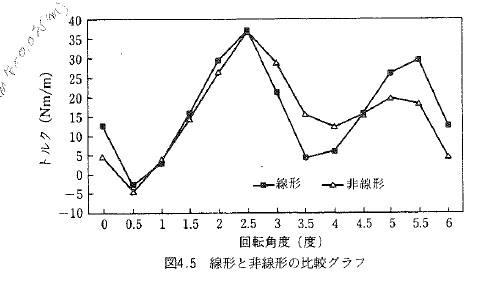
Fig.8.7.4 技法の結果(抜粋)


